|
Question 1160236: ls help me
For the function
f(x)=7/(8x+10)
find the range of by finding the values of a for which f(x)=a has a solution.
Enter your answer as an inequality
Found 2 solutions by greenestamps, ikleyn:
Answer by greenestamps(13195)   (Show Source):
You can put this solution on YOUR website!
The wording of the problem is faulty.
The equation f(x)=a has a solution for all values of x except the single value that makes the denominator 0. That value is x=-5/4.
But determining that does NOT tell us the RANGE of the function; it only tells us the DOMAIN is all values except x=-5/4.
To determine the range, we need to do some analysis.
Note that the value of the function will never be 0, because the numerator is the constant 7.
Arbitrarily large positive values of x will make the function value positive and arbitrarily small; arbitrarily large negative values of x will make the function value negative and arbitrarily small. So the range of the function includes all numbers close to 0, but not 0 itself.
The excluded value in the domain is x=-5/4. For values greater than -5/4 and arbitrarily close to -5/4, the value of the function will be arbitrarily large; so there is no upper bound on the range of the function. And for values less than -5/4 and arbitrarily close to -5/4, the value of the function will be arbitrarily "large negative"; so there is no lower bound on the range of the function.
ANSWER: The range of the function is all real numbers except 0.
Answer by ikleyn(52750)  (Show Source):
You can put this solution on YOUR website! .
You can solve the problem and get the answer following exactly instructions in your post.
You start from this equation
a =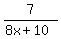 
which implies
8ax + 10a = 7
8ax = 7 - 10a
x =  .
Now you see that for EVERY value of "a", not equal to zero, you may find the solution x, according to this formula.
It EXACTLY means that the range of the function f(x) is the set of all real numbers, EXCEPT of {0}.
Solved.
It is absolutely NORMAL, REGULAR and LEGAL way to solve the problem and to get the answer.
|
|
|
| |
