SOLUTION: please help with this Calculus Max and Min question Find the critical numbers of the function. f(x) = x^4*(e^-8x)

 = 

= 



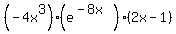
The critical points, for finite x, are at x=0 and x=1/2.



f(0) = 0                (local minimum)

f(1/2) = 0.001144727    (local maximum)



Note that f(x) is always nonnegative (x^4 is nonnegative and e^(-8x) is always positive so the product is always nonnegative). 



Here is a close up of f(x) and f'(x), zoomed way in, red graph is f'(x):