SOLUTION: Find all points on the graph of the function f(x) = 2 cos(x) + cos^2(x) at which the tangent line is horizontal. (Use n as your arbitrary integer.)

Here's the graph of f(x):

  

We want to know the coordinates of all those points (?,?) where the graph
just touches those blue and green horizontal tangent lines.

We know that tangent lines are horizontal where the derivative is zero,
so we find the derivative:



We set this derivative equal to 0:



Divide through by -2



Factor out sin(x)



Use zero factor property:

   

     
                 
                 

                 

[The equation on the right can never be true because the absolute value of
sec(x) is always 1 or greater, and the absolute value of sin(x) is always 
1 or less.  But when |sin(x)|=1, sec(x) is undefined, so they can't both
be 1.]   
                 
Thus 



When n is an even number



and when n is an odd number



So the points where the graph touches the blue and green
horizontal tangent lines are all of the form:

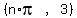 when n is an ARBITRARY even integer, and

 when n is an ARBITRARY odd integer.

Here is the graph of f(x) with those points marked for n=-3,-2,-1,0,1,2,3

 

Since 3 is 1+2 and -1 is 1-2, we can simplify the answer where n is ANY
ARBITRARY INTEGER this way:

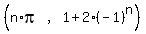 where n is ANY ARBITRARY integer. 

Edwin