|
Question 1147419: The revenue at the Assembly Center depends on the number of seats sold for the Willie Williams and the Wranglers concert. At $10 per ticket, they will fill all 8000 seats. The manager knows that for every $1 increase in the price, 500 tickets will go unsold. If the revenue in dollars, 𝑅(𝑝), is given by
𝑅(𝑝) = −500𝑝^2 + 13000𝑝, where 𝑝 is the price per ticket sold.
Find the number of unsold seats that resulted in this maximum revenue given the following 𝑛 = 13000 − 500𝑝 where 𝑛 is the number of seats sold and 𝑝 is the price.
You must show this algebraically
Answer by Theo(13342)   (Show Source): (Show Source):
You can put this solution on YOUR website! the formula given is r(p) = -500 * p^2 + 13000 * p
at 10 dollars a ticket (p = 10), the revenue will be -500 * 10^2 + 13000 * 10
that becomes -50,000 + 130,000 = 80,000.
that, however, is not the maximum revenue.
the equation given is a quadratic equation.
to find the maximum revenue, set it equal to 0 and it will be in standard quadratic equation form.
you will get:
-500 * p^2 + 13000 * p = 0
when in this form, a is equal to the coefficient of the p^2 term and b is equal to the coefficient of the p term, to get:
a = -500
b = 13000
the maximum revenue will occur at p = -b / 2a = -13000 / -1000 = 13
the maximum revenue will be when p = 13.
the formula becomes r(p) = -500 * 13^2 + 13000 * 13 = 84,500.
the number of seats will be 13 * 500 = 6,500.
this is per the formula given of n = 13,000 - 500 * p.
when p = 13, this formula becomes n = 13,000 - 500 * 13 = 13,000 - 6,500 = 6,500.
since there are 8000 seats when the stadium is full, you will have 8000 - 6500 = 1500 empty seats when the revenue is maximized.
you can graph the formula to see what's happening.
the formula for graphing the revenue is y = -500x^2 + 13000x
y replaces r(p) and x replaces p.
the formula for graphing the number of seats sold is y = 13000 - 500 * x
y replaces n and x replaces p.
the graph looks like this.
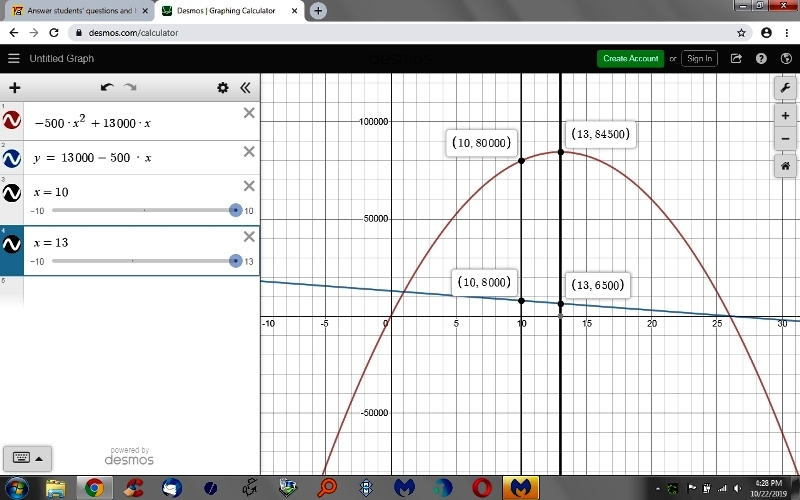
the red line is the revenue and the blue line is the number of units sold.
you can see that, when the price is 10, 8000 units are sold and the revenue is 80,000.
you can also see that, when the price is 13, 6500 units are sold and the revenue is 84500.
that's the maximum revenue and 1500 seats are empty because 8000 - 6500 = 1500.
|
|
|
| |