SOLUTION: Show by elimination that x = t^2 − 1/t^2+1 and y = 2t/ t^2+1 almost represent the unit circle x^2 + y^2 = 1. What point is missing?

Algebra ->  Functions -> SOLUTION: Show by elimination that x = t^2 − 1/t^2+1 and y = 2t/ t^2+1 almost represent the unit circle x^2 + y^2 = 1. What point is missing?       Log On


   

Question 1145113: Show by elimination that x = t^2 − 1/t^2+1 and y = 2t/ t^2+1
almost represent the unit circle x^2 + y^2 = 1. What point is missing?
Answer by ikleyn(52754) About Me  (Show Source):
You can put this solution on YOUR website!
.

After spending a significant amount of time thinking what your formulas might be, I concluded that they are


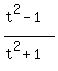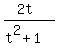    x = %28t%5E2-1%29%2F%28t%5E2%2B1%29,  y = %282t%29%2F%28t%5E2%2B1%29.


Then 


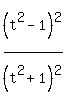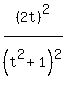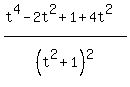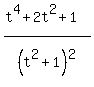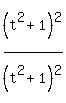    x%5E2 + y%5E2 = %28t%5E2-1%29%5E2%2F%28t%5E2%2B1%29%5E2 + %282t%29%5E2%2F%28t%5E2%2B1%29%5E2 = %28t%5E4+-+2t%5E2+%2B+1+%2B+4t%5E2%29%2F%28t%5E2%2B1%29%5E2 = %28t%5E4+%2B+2t%5E2+%2B+1%29%2F%28t%5E2%2B1%29%5E2 = %28t%5E2%2B1%29%5E2%2F%28t%5E2%2B1%29%5E2 = 1.


So, it is really an equation of the unit circle.



What point is missing ?  -------- NO point is missing.


Answered, solved and completed.

---------------- 

    Next time, when posting formulas that have a numerator and a denominator, like this one


        x = t^2 − 1/t^2+1 


    use  P L E A S E  parentheses to show explicitly which part of the formula is the numerator and which is the denominator, like this


        x = (t^2 − 1)/(t^2+1).


    Otherwise, your post is UNREADABLE (!)