|
Question 1107122: A stunt diver leaps off a bridge 50m above a river with an initial upward speed of 10m/s.
Her altitude is given by

Where t is in seconds and h is in meters.
Her average speed in one second intervals: 0-1: 5 m/s, 1-2: -5 m/s
Textbook question: Why is her average speed from t=0 to t=2 equal to zero?
My answer: 
so 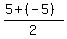
equals zero.
Next textbook question: How would you find the true average speed between t=0 and t=2 seconds?
Me: "Um, what?"
Can someone please enlighten me?
Answer by ikleyn(52754)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Let me first to re-tell the situation in my own words, instead of using formulas.
Having the initial velocity 10 m/s upward, she moves vertically up during the first second until she get the highest point
10 meters higher than her starting point was.
Her average speed at this part of the leap is 5 (five) m/s.
During the NEXT second she moves from her highest point vertically down.
During this time interval she accelerates at 10 m/s^2 from the zero velocity to 10 m/s, having the average speed
-5 m/s (directed vertically down).
You correctly added 5 m/s and -5 m/s and obtained ZERO average velocity during first two seconds.
It is CONSISTENT with the fact that to the end of the 2-nd second she is AT THE SAME HEIGHT (level) as her starting point.
And now the last step of my explanation. To answer this question
*** How would you find the true average speed between t=0 and t=2 seconds? ***
you, formally, need to calculate "the distance" h(2) - h(0), which is 50-50 = 0 meters (indeed,
she is at the same level of 50 meters at the end of the 2-nd second as she was at the beginning ! ).
And then formally to divide this zero distance by 2 seconds to get THE AVERAGE SPEED.
By doing any way, you will get the same answer.
I hope that now the issue is crystally clear to you !
|
|
|
| |