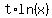

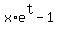 Differentiating implicitly to find
Differentiating implicitly to find 


 Clear the fraction by multiplying through by LCD=x
Clear the fraction by multiplying through by LCD=x
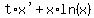


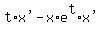

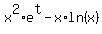


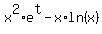
 When y is the dependent variable and x is the independent
variable, the point-slope equation of the line through
(x1,y1) with slope m is
When y is the dependent variable and x is the independent
variable, the point-slope equation of the line through
(x1,y1) with slope m is 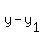

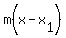 .
But in this case, x is the dependent variable and t is the independent
variable, so the equation of the line through (t1,x1)
with slope m is
.
But in this case, x is the dependent variable and t is the independent
variable, so the equation of the line through (t1,x1)
with slope m is 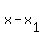

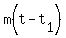 .
(t1,x1) = (0,1)
And the slope m is x' evaluated at this point:
.
(t1,x1) = (0,1)
And the slope m is x' evaluated at this point:

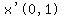


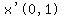

 So
So 

 So substituting m = -1, and (t1,x1) = (0,1)
So substituting m = -1, and (t1,x1) = (0,1)
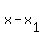

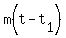


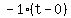


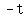


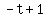 Edwin
Edwin