Question 1048554: Given f(1-x)+(1-x)f(x)=5 for all real number x, find the maximum value that is attained by f(x).
Now, this made me think really deep, but I just can't seem to analyze it.
Please help, thanks.
Answer by robertb(5830)   (Show Source):
You can put this solution on YOUR website! 
====> Replacing x by 1-x, we get 
Using Cramer's rule to find f(x),
 .
(As a check,  , which is the expression also obtained when x is replaced by 1-x in the preceding expression for f(x).)
===> f'(x) =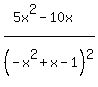 
Setting this derivative equal to 0, we get the critical values x = 0, 2.
By using the first derivative test, we find a local max at x = 0, and a local minimum at x = 2.
At x = 0, f(0) = 5.
At x = 2, f(2) = -5/3.
Therefore, the absolute max value of f(x) is 5, and the absolute min value of f(x) is -5/3.
We confirm by graphing f(x):
|
|
|
