|
Question 1041912: For  , solve for the domain and range in interval notation
I found already the domain:
(-infinity,3) u (3,+infinity)
and i'm confident that it is correct.
What confuses me is finding the Range.
I'm not confident on my answer:
(- infinity , 0] u [0, 3) u (3, + infinity)
can you give me the correct range in INTERVAL NOTATION and explain it efficiently? thanks.
Answer by josgarithmetic(39617)   (Show Source):
You can put this solution on YOUR website! Only one critical value for x, at x=3, where f is undefined.
The domain is the union, as you found.
RANGE:
What can be f, near but less than 3? What can be f, farther to the left of 3? What happens to f as x approaches 3 from the left?
Now ask and handle the same question but on the other side of x at 3.
-
Also think what happens to f as x goes unbound to the left; and what happens as x goes unbound to the right.
-
You should be able to know what is the range of f, now.
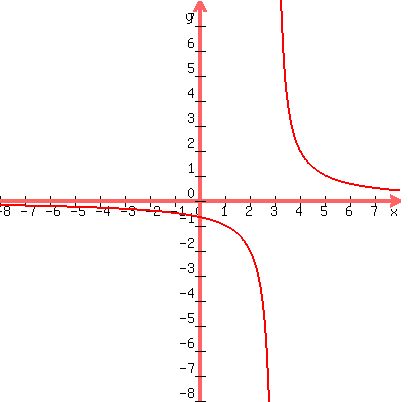
All real numbers EXCLUDING 0.
Range is (-infinity,0) AND (0, infinity).
---
(Range: I believe you have it (based on your personal message - not on what is in your posting here.)
|
|
|
| |
