Question 1209457: List all subsets of {A,B,C,D}
Found 2 solutions by math_tutor2020, ikleyn:
Answer by math_tutor2020(3828)   (Show Source): (Show Source):
You can put this solution on YOUR website!
A set is a collection of things. In this case letters A through D.
A subset is a smaller set that contains some of those letters.
It could be 0 of them, which gives the empty set. The empty set is a subset of every set.
It could be all of them. Any set is a subset of itself.
Or it could be something like {A,B,C} or {B,D}
To systematically list out every possible subset, we can use binary notation.
We count from 0 to (2^4)-1 = 15 in binary. The exponent 4 refers to the number of elements in the original set.
| Base10 | Base2 | | 0 | 0000 | | 1 | 0001 | | 2 | 0010 | | 3 | 0011 | | 4 | 0100 | | 5 | 0101 | | 6 | 0110 | | 7 | 0111 | | 8 | 1000 | | 9 | 1001 | | 10 | 1010 | | 11 | 1011 | | 12 | 1100 | | 13 | 1101 | | 14 | 1110 | | 15 | 1111 |
Counting in binary shouldn't be too tricky once you get a hang of it.
Basically you start at 0000 and increment the last digit by 1 to get 0001
Then increment the last digit of 0001 to get 0002, but the "2" doesn't exist in binary.
The only digits are 0 and 1.
A fundamental rule in binary is 12+12 = 102 or you can phrase it as saying "1+1 = 10 in binary".
This explains how we go from 0001 to 0010. The 1 carries over to the left.
Then we go from 0010 to 0011
Then from 0011 to 0100
And so on.
A recommended tool is to use the Dec2Bin spreadsheet function.
The first input of this function is the number we want to convert to binary. The second input is the number of digits for the output.
For example type in =Dec2Bin(A1,4) to convert whatever is in cell A1 to binary. It will have 4 binary digits.
There are many online calculators that can convert from decimal (base 10) to binary (base 2).
--------------------------------------------------------------------------------------------------
Why go through the trouble of using binary? Because 0 represents leaving out a particular letter while 1 represents including it.
String those 1's and/or 0's together to form a list of items.
0101 for instance means we exclude A, include B, exclude C, include D.
In short basically you have B and D to form the subset {B,D}
Another example is 1110 represents the subset {A,B,C} since we have 1's as the first three slots and 0 in the last slot.
As you can see this guarantees we do not overlook any subset.
Let's introduce a third column to the previous table that lists out all the subsets possible.
| Base10 | Base2 | Subset | | 0 | 0000 | { } | | 1 | 0001 | { D } | | 2 | 0010 | { C } | | 3 | 0011 | {C, D} | | 4 | 0100 | { B } | | 5 | 0101 | { B, D } | | 6 | 0110 | { B, C } | | 7 | 0111 | { B, C, D } | | 8 | 1000 | { A } | | 9 | 1001 | { A, D } | | 10 | 1010 | { A, C } | | 11 | 1011 | { A, C, D} | | 12 | 1100 | { A, B } | | 13 | 1101 | { A, B, D } | | 14 | 1110 | { A, B, C } | | 15 | 1111 | { A, B, C, D } |
Optionally we can sort the subsets like so
{ }
{ A }
{ B }
{ C }
{ D }
{ A, B }
{ A, C }
{ B, C }
{ A, D }
{ B, D }
{ C, D }
{ A, B, C }
{ A, B, D }
{ A, C, D }
{ B, C, D }
{ A, B, C, D }
Feel free to sort them any way you prefer.
{ } is the empty set. It has nothing inside it. Not even 0 is inside. The empty set is a subset of every set. Sometimes a special symbol is used for the empty set. The symbol looks like a zero with a slash through it.
The singletons are listed next. Singletons have 1 element as you can probably guess by the name. Then after the singletons are subsets with 2 elements. Then 3 element subsets and so on.
Since we have n = 4 slots and 2 choices per slot (either include the element or not), there are 2^n = 2^4 = 16 different subsets. The collection of all subsets is known as the Power Set.
Answer by ikleyn(53431)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
List all subsets of {A,B,C,D}
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
It has one empty subset {}.
It has 4 (four) subsets consisting of one element.
These subsets are {A}, {B}, {C}, and {D}.
It has 6 (six) subsets consisting of two elements.
These subsets are {A,B}, {A,C}, {A,D}, {B,C}, {B,D}, {C,D}.
It has 4 (four) subsets consisting of three elements.
These subsets are {A,B,C}, {A,B,D}, {A,C,D}, {B,C,D}.
We obtain this list simply crossing out letter by letter from the list of 4 elements {A,B,C,D}.
Finally, the original set {A,B,C,D} has a unique subset {A,B,C,D}, which consists of 4 elements.
This subset is special: it is called "improper" subset.
Notice that the total number of subsets is 1 + 4 + 6 + 4 + 1 = 16 = 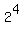 , ,
including empty subset and improper subset.
It is not a random coincidence and it is not accidently.
The general fact is that the number of all subsets of any finite set of "n" elements is  , ,
including empty subset and improper subset.
|
|
|