Question 1185955: Find the payment that should be used for the annuity due whose future value is given. Assume that the compounding period is the same as the payment period.
$20,000; quarterly payments for 17 years; interest rate 5%
the payment should be? $
Found 2 solutions by Theo, ikleyn:
Answer by Theo(13342)   (Show Source): (Show Source):
Answer by ikleyn(53431)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Find the payment that should be used for the annuity due whose future value is given.
Assume that the compounding period is the same as the payment period.
$20,000; quarterly payments for 17 years; interest rate 5% the payment should be?
~~~~~~~~~~~~~~~~~~~
What @Theo calculated for you, was the Ordinary Annuity saving plan, when the regular deposits are made at the END of each quarter.
The given problem asks about the Annuity Due saving plan, when the regular deposits are made AT THE BEGINNING of each quarter.
So, @Theo's calculations are not appropriate for this problem.
THEREFORE, I came to bring you a correct solution.
It is a classic Annuity Due saving plan. The general formula is
FV = 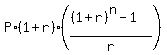 , (1)
where FV is the future value of the account; P is your quarterly payment (deposit), which is made at the beginning of each quarter;
r is the effective quarterly percentage yield presented as a decimal;
n is the number of deposits (= the number of years multiplied by 4, in this case).
Under the given conditions, FV = 20000; r = 0.05/4; n = 17*4 = 68. So, according to the formula (1), the quarterly payment should be
P = , (1)
where FV is the future value of the account; P is your quarterly payment (deposit), which is made at the beginning of each quarter;
r is the effective quarterly percentage yield presented as a decimal;
n is the number of deposits (= the number of years multiplied by 4, in this case).
Under the given conditions, FV = 20000; r = 0.05/4; n = 17*4 = 68. So, according to the formula (1), the quarterly payment should be
P = 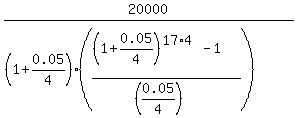 = $186.02. ANSWER
Note that you deposit only 17*4*$186.02 = $12,649.36. The rest is what the account earns/accumulates in 17 years. = $186.02. ANSWER
Note that you deposit only 17*4*$186.02 = $12,649.36. The rest is what the account earns/accumulates in 17 years.
-----------------
On Ordinary Annuity and Annuity Due saving plans, see the lessons
- Ordinary Annuity saving plans and geometric progressions
- Solved problems on Ordinary Annuity saving plans
- Solved problems on Ordinary Annuity saving plans
in this site.
The lessons contain EVERYTHING you need to know about this subject, in clear and compact form.
When you learn from these lessons, you will be able to do similar calculations in semi-automatic mode.
|
|
|