Question 999360: What is the process for finding max/min for functions?
I have this function: f(x) = 2x^3 - 3x^2 + 6. Find the max/min values of f on [-1,1]
I know that I must find all the critical points for and that is when f'=0 and the bounded pts, so, x=-1,1.
Work:
f'(x) = 6x^2 - 6x = 0
f'(x) = 6x(x-1) = 0
//6x = 0
//x=0
f'(x) = x-1 = 0
f'(x) = x = -1
Hence, x = -1,1,0,-1
So, these are all my critical values
Then I take the second derivative:
f"(x) = 12x - 6
then I plug the critical values into the second derivative, then thing that bothers me is I don't understand is why this produces a relevant result.
Work:
f"(x) = 12x - 6
f"(0) = 12(0) - 6 = -6 <0, MIN
f"(-1) = 12(-1) - 6 = -18 <0, MIN
f"(1) = 12(1) - 6 = +6 >0, MAX
At this point I hit a wall. Am I suppose to plug these output values of the 2nd derivative back into the original function. Or am I completely missing steps?
Also, another confusion I have is do the critical values represent x coordinates and the max and min represent the y coordinate and together they give (x,y)?
Thank you for any and all help!
Answer by ikleyn(52781)   (Show Source):
You can put this solution on YOUR website! What is the process for finding max/min for functions?
I have this function: f(x) = 2x^3 - 3x^2 + 6. Find the max/min values of f on [-1,1]
I know that I must find all the critical points for and that is when f'=0 and the bounded pts, so, x=-1,1.
Work:
f'(x) = 6x^2 - 6x = 0
f'(x) = 6x(x-1) = 0
//6x = 0
//x=0
f'(x) = x-1 = 0
f'(x) = x = -1
Hence, x = -1,1,0,-1
So, these are all my critical values
------------------------------------------
Hello,
till this point you acted absolutely right.
In this way you found local maximums and minimums (or, at least, the points that are candidates for local maximum
and minimum).
In addition, you need understand these two points:
1. In order to make a qualified suggestion on global maximum and minimum, you need to check and to compare also
the values of the function at the ends of the given segment. The derivatives can be non-zero there; nevertheless,
the global maximum and/or minimum can be located there.
2. Zero derivative of the given function do not necessary provides local maximum or minimum. They provide only candidates
to this role. An example is the function  at x = 0. It has the zero derivative at this point, but it is neither maximum
nor minimum. See the plot below.
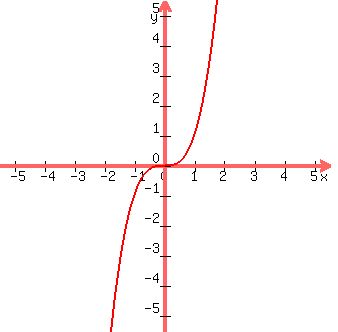
Figure. Plot y =
|
I am continuing.
----------------------------------------------------------------
Then I take the second derivative:
f"(x) = 12x - 6
then I plug the critical values into the second derivative, then thing that bothers me is I don't understand is why this produces a relevant result.
Work:
f"(x) = 12x - 6
f"(0) = 12(0) - 6 = -6 <0, MIN
f"(-1) = 12(-1) - 6 = -18 <0, MIN
f"(1) = 12(1) - 6 = +6 >0, MAX
At this point I hit a wall. Am I suppose to plug these output values of the 2nd derivative back into the original function. Or am I completely missing steps?
Also, another confusion I have is do the critical values represent x coordinates and the max and min represent the y coordinate and together they give (x,y)?
Thank you for any and all help!
----------------------------------------------------------------
The second derivatives helps you and serves you to determine if the plot of the function is convex downward or concave upward.
If the second derivative is positive then the function (or the plot of the function) is convex downward (like  ).
If the second derivative is negative then the function (or the plot of the function) is concave upward (like  ).
So, the second derivative helps you to determine, if your candidate to the local minimum or the local maximum is real local
minimum or local maximum.
Is this explanation clear to you?
Please let me know. You may put your answer in the "Comments for students" section.
If you do, do not forget to put the number of the problem (# 999360) in order I could identify it.
Thank you.
|
|
|
