SOLUTION: State the vertical, horizontal asymptotes and zeros of the rational function, f(x) = (x^2 + 3x + 2)/(x^2 + 5x + 4) Why is there no zero at x = –1?

Instead of doing your problem for you, I'll do one exactly in every detail
like yours so that you can do yours yourself using this as a model.  You
won't learn it as well if I do it for you. I'll do this one instead:

First we'll get the horizontal asymptote's equation:

Since the numerator and denominator have the same degree, the horizontal
asymptote's equation is 
   
That's



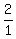
Now let's answer the question "Why is there no zero at x = –3?"
Let's substitute -2 for x and see:






One of the impossible things in mathematics is division
by zero.  So that's why I crossed this out, and it's why f(-3)
is not a zero.

Now we'll go back and find the vertical asymptotes



We factor numerator and denominator:



Now since the (x+3)'s will cancel, that will give us another function g(x)
which is exactly like f(x) except it WILL have a zero at x=-3 whereas f(x)
does not have a zero there:

So we get



And we find the vertical asymptote's equation by setting the denominator = 0:

x+4 = 0

So the vertical asymptote's equation is x = -4

Now we graph g(x) by graphing the horizontal and vertical asymptotes (in green)
and making a table of values:

 x   y
-14  2.5
-9   3
-5   7
-3  -3
 0   1
 6  1.5    
  


That's the graph of g(x) but the graph of f(x) must
have a hole at (-3,-3) because that's not part of the
graph:



Edwin