Question 979438: How do i find the zeros of this equation 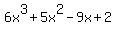
I have tried to factor out an x and than factor it as i would with
a normal quadratic but i reached this answer 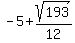 and and
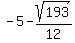 and i needed to multiply the x back in but i and i needed to multiply the x back in but i
did not know how to or what i should do after that. also because this is a
3rd degree polynomial than shouldn't it have 3 zeros. if possible please
show me step by step how to do this , thank you so much
Found 2 solutions by KMST, Fombitz:
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! If 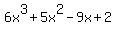 has a rational zero, has a rational zero,
you should be able to use it to factor the polynomial,
and find the exact value of all of its real zeros.
If 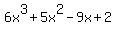 does not have a rational zero, does not have a rational zero,
you could only find approximate values by guided trial and error.
If 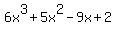 has a rational zero has a rational zero 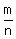 , it must be that , it must be that
 is a factor of the constant term is a factor of the constant term  , and , and
 is a factor of the leading coefficient is a factor of the leading coefficient  . .
Factors of  are are  , and , and  . .
Factors of  are are  , ,  , ,  , and , and  . .
The possible values for 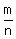 are are
-2, -1, -2/3, -1/3, -1/6, 1/6, 1/3, 2/3, 1, and 2.
You are expected to use synthetic division
(long division works too, but uses more ink)
to find that  is a zero. is a zero.
(The other nine possible values are not zeros).
Synthetic division tells you
not only that 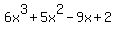 is zero for is zero for  , ,
but also that
 <---> <--->
The other two zeros of 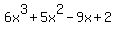 are the zeros of are the zeros of 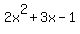 . .
You can find if they are real zeros, and their value by solving
 . .
You could do that by completing the square, or by applying
the quadratic formula  , ,
which gives the solutions to 
In this case, with  , the solutions to , the solutions to  are are

Answer by Fombitz(32388)   (Show Source): (Show Source):
|
|
|