Question 949625: Please help me to solve this problem:
Mark takes out a loan of 40,000 that is must be repaid over the course of 5 years. Interest is compounded at a nominal rate of 9% convertible monthly and he makes 60 scheduled repayments of 735 at the end of each month. What additional payment must he make at the end of the term so that the loan is completely paid off?
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website!  nominal rate convertible monthly means that nominal rate convertible monthly means that
each  of the year (1 month) they add of the year (1 month) they add  of of 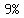 , ,
that is  times the old balance, times the old balance,
to the old balance to calculate the new balance.
At the end of the first month, just as Mark is about to make his first payment,
they add 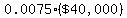 to the to the 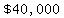 to get to get
 , ,
which is 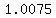 times the previous balance. times the previous balance.
Immediately, Mark makes his 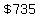 payment, and the balance goes down to payment, and the balance goes down to
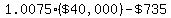 . .
At the end of the second month, just as Mark is about to make his second payment,
the balance again increases by a factor of 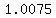 , ,
from 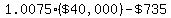 to to 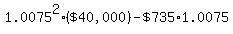 , ,
only to get immediately reduced by the second 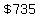 payment payment
to 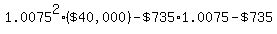 . .
At the end of the second month,
the balance first increases again by a factor of 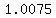 , ,
to 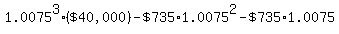 , and then , and then
decreases to 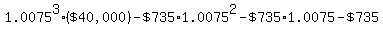
with the third 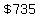 payment. payment.
The pattern repeats each month, so after  months, and months, and  payments, the balance is payments, the balance is
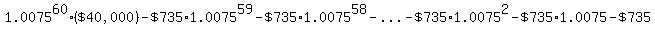
=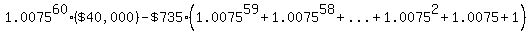
From either geometric sequences and series,
or from polynomial s and factoring, we know that
 . .
So the final balance, after  months, and months, and  payments is payments is

|
|
|