Question 930358: Please explain how to find the reference angle for the given angle:
5π/4
-5π/6
5π/3
Thank you
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! EXPLANATION:
The reference angle is the first quadrant angle,
an angle  such that such that

(for the radian-impaired, that is  ). ).
It is an angle whose trigonometric functions have the same absolute value
(you may have to change the sign to a negative sign).
It is an angle whose terminal side is symmetrical,
meaning it is reflected over the y-axis for angles in the second quadrant;
it is reflected over the x-axis for angles in the fourth quadrant,
and it is symmetrical with respect to the origin for angles in the third quadrant.
 Angle Angle  is the reference angle for angles is the reference angle for angles
 in the second quadrant, in the second quadrant,
 in the third quadrant, and in the third quadrant, and
 in the fourth quadrant. in the fourth quadrant.
EXAMPLE 1:
Expressing the boundaries of the quadrants as multiples of  for your convenience, for angles between for your convenience, for angles between  and and  , ,
 is the first quadrant; is the first quadrant;
 is the second quadrant; is the second quadrant;
 is the third quadrant, is the third quadrant,
and  is the fourth quadrant. is the fourth quadrant.

What quadrant is  in? in?
Since  , ,  is the third quadrant, is the third quadrant,
so its reference angle is  . .
EXAMPLE 2:
What quadrant is 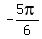 in? in?
Since  , ,
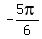 is also in the third quadrant. is also in the third quadrant.
 is the reference angle. is the reference angle.
|
|
|