Question 891622: Determine whether the given x-value is a solution of the equation.
x/2x+1 = 5/4-x^2 , x=-1
True
False
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! I assume the equation is really
x/(2x+1)= 5/(4-x^2) or  . .
(If you cannot write the  and the and the 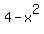 as denominators, as denominators,
under long horizontal lines,
the only way to show that those deonminators need to be calculated first is to wrap them in parentheses).
Substituting  into that equation we get into that equation we get
 , which is , which is
 , ,
 , and , and
 . .
That is false.
The equation you wrote is
x/2x+1 = 5/4-x^2 or  , ,
which is different, because without the parentheses,
 is calculated first, before adding is calculated first, before adding  . .
For that equation, substituting  gives us gives us
 , which is , which is
 , and , and
 . .
That is also false.
|
|
|