SOLUTION: Determine which two functions are inverse of each other. {{{ f(x)= (x-7)/3 }}} {{{ g(x)=3x-7 }}} {{{ h(x)=(x-3)/(-7) }}}

Algebra ->  Finance -> SOLUTION: Determine which two functions are inverse of each other. {{{ f(x)= (x-7)/3 }}} {{{ g(x)=3x-7 }}} {{{ h(x)=(x-3)/(-7) }}}      Log On


   

Question 691436: Determine which two functions are inverse of each other.
+f%28x%29=+%28x-7%29%2F3+
+g%28x%29=3x-7+
+h%28x%29=%28x-3%29%2F%28-7%29+
Answer by mouk(232) About Me  (Show Source):
You can put this solution on YOUR website!
A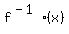) +f%28x%29=+%28x-7%29%2F3+, we find +f%5E%28-1%29%28x%29+ by setting +y+=+%28x-7%29%2F3+ and rearranging to make x the subject, so
+%28x-7%29%2F3+=+y+
+x-7+=+3y+
+x=3y%2B7+
and replacing y with x gives us the inverse
Hence, +f%5E%28-1%29%28x%29+=+3x%2B7
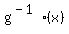B) +g%28x%29=+3x-7+, we find +g%5E%28-1%29%28x%29+ by setting +y+=+3x-7+ and rearranging to make x the subject, so
+3x-7+=+y+
+3x+=+y%2B7+
+x=%28y%2B7%29%2F3+
and replacing y with x gives us the inverse
Hence, +g%5E%28-1%29%28x%29+=+%28x%2B7%29%2F3+
C) +h%28x%29=+%28x-3%29%2F%28-7%29+, we find +h%5E%28-1%29%28x%29+ by setting +y+=+%28x-3%29%2F%28-7%29+ and rearranging to make x the subject, so
+%28x-3%29%2F%28-7%29+=+y+
+x-3+=+-7y+
+x=3-7y+
and replacing y with x gives us the inverse
Hence, +h%5E%28-1%29%28x%29+=+3-7x+
Conclusion: none of the functions are inverses of each other. Is there a typo in the question? Let me know and I'll take another look.
Kind Regards, Steve.