SOLUTION: Decide whether or not the points are the vertices of a right triangle. (-1,-7),(5,-5),(9,-17)

A(-1,-7),B(5,-5),C(9,-17)



It looks like a right triangle, because angle B looks
like a 90° angle.  But it's not acceptable to just say
it looks like a right triangle, we have to show that B
is a right angle.  We need to show that AB is perpendicular
to BC.  To do that we find their slopes, and see if their
product is -1, or if one is the reciprocal of the other
with the opposite sign:

We find the slope of AB 

m =  =  =  =  =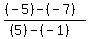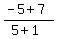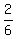 

We find the slope of BC  A(-1,-7),B(5,-5),C(9,-17)

m =  =  =  =  =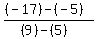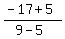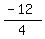 

So we see that -3 is the reciprocal of  with the opposite sign
or, you can say the slopes have product ·(-3) = -1.

So AB and BC are perpendicular and therefore B is a right angle, and
therefore ABC is a right triangle.

Edwin