Question 1209197: Megan wants to buy an item worth $400. She has two coupons of 10% and 15% off. What is the total discount rate, as a percentage, if she used both coupons? Hint: The answer is not 25%
Found 2 solutions by ikleyn, math_tutor2020:
Answer by ikleyn(52785)   (Show Source):
You can put this solution on YOUR website! .
First coupon reduces the buying price from $400 to (1-0.1)*400 = 0.9*400 = 360 dollars.
Second coupon reduces the buying price from $360 to (1-0.15)*360 = 0.85*360 = 306 dollars.
The total discount rate of the two coupons is 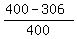 = 0.235.
Notice the remarkable fact that this value of 0.235 coincides with
1 - (1-0.1)*(1-0.75) = 1 - 0.9*0.85 = 0.235.
It explain you an idea on HOW TO calculate an effective discount rate for a chain of discounts.
Solved.
Answer by math_tutor2020(3817)  (Show Source):
You can put this solution on YOUR website!
Answer: 23.5%
Work Shown
a = 0.10 represents the 10% discount rate
b = 0.15 is the 15% discount
The order of a,b doesn't matter.
(1-a)*(1-b) = proportion Megan spends
1-(1-a)*(1-b) = proportion Megan saves
1-(1-a)*(1-b) = 1-(1-0.10)*(1-0.15) = 0.235 = 23.5% is total discount rate as a percentage. This value is exact and hasn't been rounded.
This idea can be extended to more than two discounts.- 3 discounts: 1-(1-a)*(1-b)*(1-c)
- 4 discounts: 1-(1-a)*(1-b)*(1-c)*(1-d)
- 5 discounts: 1-(1-a)*(1-b)*(1-c)*(1-d)*(1-e)
- And so on.
a,b,c,d,e,... represent the individual discount rates in decimal form between 0 and 1 excluding both endpoints.
The final result will be in decimal form between 0 and 1. Multiply by 100 to convert to a percentage. This is equivalent to moving the decimal point two spots to the right (eg: 0.1234 converts to 12.34%)
-------------
Another approach.
Megan spends 400*(1-0.10)*(1-0.15) = 306 dollars
She saves 400-306 = 94 dollars.
Then 94/400 = 0.235 = 23.5% is the combined discount rate.
Note that the 400 can be changed to any other positive number to get the same result at the end.
Therefore the starting price will not affect the answer.
-------------
This section will discuss yet another approach.
It's a bit slower, but it's always a good idea to be able to look at math problems from multiple viewpoints.
The item starts off at $400
Let's say Megan uses the 10% discount first.
She saves 0.10*($400) = $40 and the price is now $400 - $40 = $360
Or as a slight shortcut we could say 0.90*($400) = $360 since saving 10% means she pays the remaining 90%.
Now she'll use the 15% discount.
She saves an extra 0.15*($360) = $54 and the final price is $360 - $54 = $306
Overall Megan saves $400 - $306 = $94 (or add the discounts 40+54 = 94)
Divide this total savings over the original starting price to get the combined discount rate
94/400 = 0.235 = 23.5% which is the final answer.
-------------
The 23.5% is somewhat close to 25% which was mentioned in the hint.
A first-time student's approach would likely say 10% + 15% = 25%
But that is not correct.
Why can't we add the percentages? Because the second discount does NOT apply to the original $400; instead it applies to the reduced cost of some value less than $400.
I've seen many students make the common mistake of adding the percentages when trying to find the total discount rate. Be careful to avoid this trap.
What if Megan swapped the order of the discounts?
Let's say she used the 15% discount first.
She saves 0.15*($400) = $60 and the price is now $400 - $60 = $340
Next she'll use the 10% discount.
She saves another 0.10*($340) = $34 and the final price is $340 - $34 = $306
We arrive at the same final price of $306.
It turns out the order of the discounts does not matter.
Refer back to the template 1-(1-a)*(1-b) to see that we can multiply (1-a) and (1-b) in either order.
|
|
|
