Question 120868This question is from textbook college algebra
: Could you please help solve for this problem it has 4 parts? I don't know where to start.
The path of a falling object is given by the function s=-16t^2+v0t+s0 where v0 represents the initial velocity in ft/sec and s0 represents the initial height. The variable t is time in seconds, and the s is the height of the object in feet.
a) If a rock is thrown upward with an initial velocity of 32 feet per second from the top of a 40-foot building, write the height equation using this information.
b) How high is the rock after 0.5 seconds?
c) After how many sections will the rock reach maximum height?
d)What is the maximum height?
Please show all work
Thanks in advance for your help.
This question is from textbook college algebra
Found 2 solutions by stanbon, solver91311:
Answer by stanbon(75887)   (Show Source): (Show Source):
You can put this solution on YOUR website! The path of a falling object is given by the function s=-16t^2+v0t+s0 where v0 represents the initial velocity in ft/sec and s0 represents the initial height. The variable t is time in seconds, and the s is the height of the object in feet.
a) If a rock is thrown upward with an initial velocity of 32 feet per second from the top of a 40-foot building, write the height equation using this information.
s(t)=-16t^2+32t+40
--------------------------------
b) How high is the rock after 0.5 seconds?
s(0.5) = -16(0.5)^2+32(0.5)+40 = 50 ft.
----------------------------------
c) After how many seconds will the rock reach maximum height?
Maximum occurs when t = -b/2a = -32/(2*-16) = 1 second
-----------------------------------
d)What is the maximum height?
Maximum height occurs at s(1) = -16+32+40 = 56
====================================
Cheers,
Stan H.
Answer by solver91311(24713)   (Show Source): (Show Source):
You can put this solution on YOUR website! 
a. You are given that  and and  , so just plug in the values: , so just plug in the values:

b. You need to evaluate 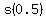




So the height (measured from the ground) after one-half second is 52 feet.
c. This is a quadratic equation and if you graphed it on a coordinate plane with s as the vertical axis and t as the horizontal axis, you would have a convex down parabola. The maximum height will be reached at time equal to the value of t at the vertex of the parabola.
The vertex of any parabola described by  is located at ( is located at ( , ,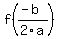 ) )
For this problem,  and and  , hence , hence  second. second.
================================================
You can also do this part with the calculus
A local minimum or maximum is found where the first derivative equals 0.
For this problem, s'(t)=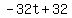 , so if , so if  then then 
To determine if this is a maximum or minimum, evaluate the second derivative at the same value
s"(t)=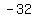 . Since the second derivitive is less than zero, this is a maximum. . Since the second derivitive is less than zero, this is a maximum.
=================================================
d. The actual maximum height is just the function evaluated at the time for maximum height, i.e. 1 second, or 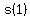



And the maximum height is 56 feet.
|
|
|