Question 1206260: ou have 50000 to invest and requier an annual return of 7000. you can invest your money in bonds, which pay a return of 15% per year, or you can invest in a certificate of deposit which pays 7% per year. how much money should you invest in each to realize exactly $7000 in interest per year?
Found 2 solutions by ikleyn, greenestamps:
Answer by ikleyn(52781)   (Show Source):
You can put this solution on YOUR website! .
ou have 50000 to invest and requier an annual return of 7000. you can invest your money in bonds,
which pay a return of 15% per year, or you can invest in a certificate of deposit which pays 7% per year.
how much money should you invest in each to realize exactly $7000 in interest per year?
~~~~~~~~~~~~~~~~~~~
Let x be the amount to invest at 15% per year.
Then the rest, (50000-x) dollars, you invest at 7% per year.
x dollars at 15% generate 0.15x dollars as the interest.
(50000-x) dollars at 7% generate 0.07(50000-x) dollars as the interest.
You want two separate interests sum up to 7000 dollars
0.15x + 0.07*(50000-x) = 7000 dollars.
Simplify this equation and find x
0.15x + 0.07*50000 - 0.07x = 7000
0.15x - 0.07x = 7000 - 0.07*50000
0.08x = 3500
x = 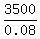 = 43750.
At this point, the problem is just solved.
ANSWER. $43750 should be invested at 15% and the rest 50000-43750 = 6250 dollars should be invested at 7%.
Solved.
Answer by greenestamps(13200)  (Show Source):
You can put this solution on YOUR website!
The other tutor has shown a good typical formal algebraic solution.
For any 2-part "mixture" problem like this, there is another (informal) method that is usually faster than solving an algebraic equation. For this problem....
(1) Calculate that a return of $7000 on an investment of $50000 is a rate of 14%.
(2) Using a number line if it helps, observe/calculate that 14% is 7/8 of the way from 7% to 15%.
(3) That means 7/8 of the total $50000 needs to be invested at the higher rate.
ANSWERS: (7/8) of $50000 = $43750 at 15%; (1/8) of $50000 = $6250 at 7%
CHECK: .15($43750)+.07($6250) = $6562.50+$437.50 = $7000
|
|
|
