Question 1205743: On some busy streets, diamond lanes are reserved for taxis, buses, and cars with three or more passengers. It is estimated that 20% of cars travelling in a certain diamond lane have fewer than three passengers. If 60 cars that travel in a certain diamond lane are selected at random, find the probability that:
a. fewer than 10 cars have less than 3 passengers.
b. at least 15 cars have fewer than 3 passengers.
(Please help)
Answer by ikleyn(52781)   (Show Source):
You can put this solution on YOUR website! .
On some busy streets, diamond lanes are reserved for taxis, buses, and cars
with three or more passengers. It is estimated that 20% of cars travelling
in a certain diamond lane have fewer than three passengers.
If 60 cars that travel in a certain diamond lane are selected at random, find the probability that:
(a) fewer than 10 cars have less than 3 passengers.
(b) at least 15 cars have fewer than 3 passengers.
~~~~~~~~~~~~~~~~~~~~~~~~~~~
Obviously, this problem is on the binomial distribution.
The number of trials is n= 60; the probability of the success (fever than 3 passengers) is p= 0.2.
The number of success trials k is k<10 in part (a) and k>=15 in part (b).
Since the number of trials, 60, is great, it is recommended to use the normal approximation to
the binomial approximation.
In this normal approximation, the mean is mean = np = 60*0.2 = 12; the standard deviation
SD = 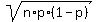 =  = 3.098386677.
In part (a), you should find a normal distribution probability to get k<10.
We can use a regular hand calculator TI-83/84 with standard function normalcfd
z1 z2 mean SD <<<---=== formatting pattern
P = normalcfd(-9999, 10.5, 12, 3.098386677). (1)
Here 10.5 is the continuity correction factor to the number of 10.
The ANSWER (the value of (1)) is the probability P = 0.3141 (rounded).
Alternatively, to find the value of (1), you may use the online calculator at web-site
https://onlinestatbook.com/2/calculators/normal_dist.html
It has very convenient simple interface, so even a beginner student can use it without further
explanations. This calculator will produce the same answer (the same value of probability).
Solve part (b) in the same way. In part (b), use the value of 14.5 as the continuity correction factor for the number 15.
Solved.
|
|
|
