SOLUTION: You have $400,000 saved for retirement. Your account earns 8% interest. How much will you be able to pull out each month, if you want to be able to take withdrawals for 25 years?

Algebra ->  Finance -> SOLUTION: You have $400,000 saved for retirement. Your account earns 8% interest. How much will you be able to pull out each month, if you want to be able to take withdrawals for 25 years?       Log On


   

Question 1204183: You have $400,000 saved for retirement. Your account earns 8% interest. How much will you be able to pull out each month, if you want to be able to take withdrawals for 25 years?
$
Found 2 solutions by MathLover1, ikleyn:
Answer by MathLover1(20849) About Me  (Show Source):
You can put this solution on YOUR website!

Recall that the formula for the present value of the ordinary annuity,

P=%28x%2Fi%29%281-%281%2Bi%29%5E%28-nk%29%29
if
P=400000
i%2F12=8%2F12=2%2F3%=%281%2F150%29%2F12=1%2F1800=> (monthly)
n=25
k=12 (months)
then
400000=%28x%2F%281%2F1800%29%29%281-%281%2B1%2F1800%29%5E%28%28-25%2A12%29%29%29

400000=%281800x%29%281-0.8465209002574435%29

400000=%281800x%29%280.15347909974255647%29

400000=276.26237953660165+x

x=400000%2F276.26237953660165

x=1447.90

you would be able to withdraw 1447.90 each month for 25+years


Answer by ikleyn(52781) About Me  (Show Source):
You can put this solution on YOUR website!
.
You have $400,000 saved for retirement. Your account earns 8% interest.
How much will you be able to pull out each month, if you want to be able to take withdrawals for 25 years?
~~~~~~~~~~~~~~~~~~~~~~~~~


        This problem is posed incorrectly. To be correct, the problem must to point WHEN the withdrawals
        are made, at the end or at the beginning of each compounding period (which is month).
        Usually/traditionally, in such problems it is assumed that the withdrawals are made at the BEGINNING
        of each month for living. So I will follow this hypothesis. But I should notice, with the DEEP SORROW,
        that the creators of this problems do not know the basics of the subject and are not able to pose the problem in a right way. 


Use the general formula  A = W%2Ap%2A%28%281-p%5E%28-n%29%29%2Fr%29.


Here A is the initial amount at the account; W is the monthly withdrawn value at the beginning of each month; 
r is the nominal monthly percentage r = 0.08/12 presented as a decimal;  
p = 1 + r  and n is the number of withdrawing periods (months, in this case).


In this problem,  W is the unknown;  the monthly rate is  r = 0.08/12,  
p = 1 + 0.08/12, the number of payment periods (= the number of months) is n = 25*12 = 300.  So


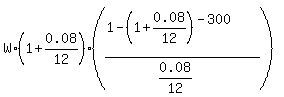          400000 = W%2A%281%2B0.08%2F12%29%2A%28%281-%281%2B0.08%2F12%29%5E%28-300%29%29%2F%280.08%2F12%29%29.


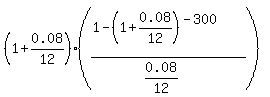The factor  %281%2B0.08%2F12%29%2A%28%281-%281%2B0.08%2F12%29%5E%28-300%29%29%2F%280.08%2F12%29%29 is equal to 130.4282861;  therefore


           W = 400000%2F130.4282861 = 3066.82 dollars.


Thus you will be able to withdraw $3066.82 every month (at the beginning of each month) during 25 years.

Solved.

--------------------

In this site,  there is a group of lessons associated with annuity saving plans and retirement plans.  They are

    - Ordinary Annuity saving plans and geometric progressions
    - Annuity Due saving plans and geometric progressions
    - Solved problems on Ordinary Annuity saving plans
    - Withdrawing a certain amount of money periodically from a compounded saving account (*)
    - Miscellaneous problems on retirement plans

From these lessons,  you can learn the subject and can see many similar solved problems.

The closest lesson to your problem is marked (*) in the list.