SOLUTION: the hourly wage of some toyota automobile assembly line workers is being increased annually by the same percentage if their wage went from 7.10 to 20.08 in 12 years. what is the do

According to the problem, for the annual salary we have this exponential equation

    y = 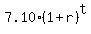,  where "t" denotes years from the starting moment.


We want to find (1+r), the coefficient of growth.
At t= 12 we have

    20.08 = .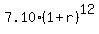


Divide both sides by 7.10

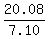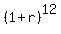     = ,  or

    2.828169014 = .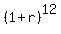


Take logarithm base 10 of both sides

    log(2.828169014) = 12*log(1+r)

    log(1+r) = 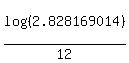 = 0.037625447.


Hence,

    1+r = 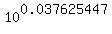 = 1.09049944.


Thus we just found out the coefficient of growth.


To find the doubling period, we shoud find "t" from this equation

    2 = ,  or

    2 = .


Again, take logarithm base 10 of both sides

    log(2) = t*log(1+r).


We just found out the value of log(1+r) above: it is  0.037625447.


Therefore, the doubling time is  t = 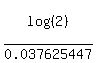 = 8.000702 years,
which we can round to 8 years.


ANSWER.  The doubling period is 8 years.