Question 120323: Wilma wants to have $2,000,000.00 when she retires in 45 years. Assuming that she can average 4.5% return anually in treasury bills, then how much must she invest now in treasury bills to achieve her goal?
This is how I worked it:
0.045X x 45 = 2,000,000
0.045X = 44444.44
X = 987653.33
Found 2 solutions by solver91311, Fombitz:
Answer by solver91311(24713)   (Show Source): (Show Source):
You can put this solution on YOUR website! Look at it this way:
Let x be the amount of the initial investment.
If Wilma gets 4.5% annual return, then the first year she gets .045x dollars in interest, so the total amount in her account at the end of the first year is x + .045x dollars. Another way to write that is  , where , where 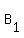 is the balance at the end of 1 year. is the balance at the end of 1 year.
At the end of the second year, where she will have started with 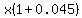 , she will have , she will have 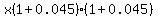 , and so on, through the years, multiplying the previous amount by an additional factor of , and so on, through the years, multiplying the previous amount by an additional factor of 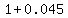 each year. each year.
Shorthand for multiplying several identical factors is raising that factor to a power, so at the end of two years she will have 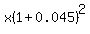 , at the end of three years she will have , at the end of three years she will have 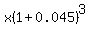 , and finally at the end of 45 years she will have , and finally at the end of 45 years she will have 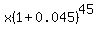 . .
We want this amount to be $2 Million. So set the expression equal to 2000000.

Now solve:

Plugging these values into a spreadsheet gives 
The only way to check this answer conveniently is to compare the answer to an estimate and see if it is reasonable. To do this, there is a convenient rule of thumb called the Rule of 72. The Rule of 72 says that if you divide the number 72 by the annual rate of return, you get an approximation of the number of years it takes for your principal to double.
 , which means that an investment at 4.5% should double every 16 years. , which means that an investment at 4.5% should double every 16 years.
First 16 years: 
2nd 16 years: 
3rd 16 years: 
 , so using the rule of 72, you should have about $2.2 million after 48 years at 4.5%. $2 million after 45 years seems rather reasonable. , so using the rule of 72, you should have about $2.2 million after 48 years at 4.5%. $2 million after 45 years seems rather reasonable.
Hope this helps,
John
Answer by Fombitz(32388)   (Show Source): (Show Source):
You can put this solution on YOUR website! You have to take interest compounding into account.
Every year, you make interest to add to your sum and then in the following year, you get interst on the new sum, and so on.
The formula is,

where FV is the future value, P is the current investement, R is the rate of return, and T is the number of time periods.
FV=$2,000,000
R=4.5%
T=45 years




To reach her goal in 45 years, she should invest $275,928.73.
|
|
|