Question 1203212: A trucking company determined that the distance traveled per truck per year is normally distributed, with a mean of 30 thousand miles and a standard deviation of 8 thousand miles. How many miles will be traveled by at least 75% of the trucks?
Found 2 solutions by Theo, ikleyn:
Answer by Theo(13342)   (Show Source): (Show Source):
You can put this solution on YOUR website! population mean = 30,000
population standard deviation = 8,000
number of miles traveled by at least 75% of the trucks is equal to 24604.
this is what it looks like on a normal distribution graph.

Answer by ikleyn(52787)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
A trucking company determined that the distance traveled per truck per year is normally distributed,
with a mean of 30 thousand miles and a standard deviation of 8 thousand miles.
How many miles will be traveled by at least 75% of the trucks?
~~~~~~~~~~~~~~~~~~~~~~~
As the problem is worded, printed, posted and presented, it is TOTAL, GLOBAL and FATAL  . .
This my statement means that this formulation is nonsensical and the problem CAN NOT be solved in this formulation.
The fact that Theo produced some text, even with a figure, does not make this nonsense more sensical.
If you want to create something sensical from this text, then the problem should sound THIS WAY:
A trucking company determined that the distance traveled per truck per year is normally distributed,
with a mean of 30 thousand miles and a standard deviation of 8 thousand miles.
Let X denotes some distance and let D(X) denotes the integral distance, traveled
by all the company's trucks altogether, that covered more than X miles each (individually).
Find the value X such that D(X) is 75% of D, the total integral distance,
traveled by all the trucks of the company, altogether.
Do you like this bulky formulation or not, but it is the ONLY WAY (a-UNIQUE-WAY)
to make a sensible problem from the original nonsensical set of words.
And if you accept this my formulation, then the solution is as follows.
For any X, D(X) is the area under the given (specified) normal curve on the right of z-mark X.
So, the problem (in modified formulation ) asks to find the value 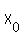 in such away,
that the area under the specified normal curve on the right of in such away,
that the area under the specified normal curve on the right of 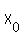 is 75% = 0.75
of the total area under this curve, i.e. simply 0.75.
To find is 75% = 0.75
of the total area under this curve, i.e. simply 0.75.
To find 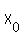 , we use the standard function invNorm
area mean SD <<<---=== formatting pattern. , we use the standard function invNorm
area mean SD <<<---=== formatting pattern.
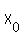 = invNorm(0.25, 30000, 8000).
I use the area value 0.25, because function invNorm accept the area on the left of the mark, and 0.25 = 1-0.75.
Thus, the ANSWER is = invNorm(0.25, 30000, 8000).
I use the area value 0.25, because function invNorm accept the area on the left of the mark, and 0.25 = 1-0.75.
Thus, the ANSWER is 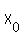 = 24604 miles. = 24604 miles.
Solved.
|
|
|