Question 1203115: Write the relation for a parabola, in vertex form, that satisfies each condition. State your reasoning!
a.)
Vertex at (-3, 2), reflected about x-axis and has the step pattern: -3, -9, -15
b.)
The graph opens upwards, is wider than y = x² and has no zeros. There is more than 1 right answer.
Found 3 solutions by math_tutor2020, ikleyn, greenestamps:
Answer by math_tutor2020(3817)   (Show Source):
You can put this solution on YOUR website!
I'll do part (b) to get you started.
The standard form of a quadratic is
y = ax^2+bx+c
The 'a' coefficient handles whether the parabola opens up or down.
a > 0 opens upward
a < 0 opens downward
We're told the mystery graph opens upward, so a > 0
The mystery graph is wider than y = x^2 aka y = 1x^2
This must mean 0 < a < 1
For example, if a = 0.5 then y = 0.5x^2 is wider than y = x^2
The closer 'a' gets to zero, the more wide and spread out the parabola gets.
As 'a' gets further from 0, the parabola narrows and gets taller.
I strongly recommend using a tool like Desmos or GeoGebra to play around with the equation y = a*x^2, where 'a' is set up to be a parameter. Slide the parameter values around to see the parabola change shape.
Here's a link to what I mean
https://www.desmos.com/calculator/ozfuw6m6ty
The slider for parameter 'a' is found in the left panel.
Moving that slider around will change the blue parabola.
Now because this mystery parabola does not have any zeros (aka roots), this must mean there aren't any x intercepts. We'll add some positive value to y = ax^2 to get to y = ax^2+c
This moves the parabola upward c number of units to ensure the parabola never touches the x axis.
For example we could have y = 0.5x^2+7
Another example would be y = 0.36x^2+1
There are infinitely many options here.
Just make sure that 0 < a < 1 and c > 0.
Answer by ikleyn(52781)  (Show Source):
You can put this solution on YOUR website! .
There are infinitely many answers to this question (b).
The general form of such parabola is
f(x) = 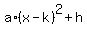 , 0 < a < 1, h > 0, k is any real number.
Answer by greenestamps(13200)  (Show Source):
You can put this solution on YOUR website!
Regarding your first example, which was not addressed in either response you have received so far....
(1) "reflected about x-axis..." ?? Non-standard language -- does that mean the parabola opens downward?
(2) -3, -9, -15 is a linear step pattern -- not a quadratic one
|
|
|
