Question 1202025: Find the equation of a circle that passes through (2,0) and (8,0) and also touches the Y-axis
Answer by ikleyn(52824)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Find the equation of a circle that passes through (2,0) and (8,0) and also touches the Y-axis
~~~~~~~~~~~~~~
The given points A = (2,0) and B = (8,0) are two points in x-axis. They are x-intercept points.
Since the circle passes through these two points, its radius lies on the perpendicular
to x-axis, which bisects the interval between the points A and B.
It means that x-coordinate of the center is x= 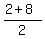 = =  = 5.
Next, since the circle touches y-axis, the radius of the circle is 5 units.
In the circle, we have a cord AB of the length 8-2 = 6; half of the chord has the length 6/2 = 3.
Then y-coordinate of the center is = 5.
Next, since the circle touches y-axis, the radius of the circle is 5 units.
In the circle, we have a cord AB of the length 8-2 = 6; half of the chord has the length 6/2 = 3.
Then y-coordinate of the center is  = =  = 4.
Thus the equation of the circle in standard form is = 4.
Thus the equation of the circle in standard form is
 + + 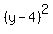 = 5^2,
or = 5^2,
or
 + + 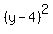 = 25. ANSWER = 25. ANSWER
Solved.
|
|
|