Question 1200963: Asset X generates a perpetual stream of cash flows of $100,000 every 3 months. The relevant interest rate is 12%, compounded quarterly. How much would you pay to buy Asset X today if the first payment occurs right away?
Answer by ikleyn(52781)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Asset X generates a perpetual stream of cash flows of $100,000 every 3 months.
The relevant interest rate is 12%, compounded quarterly.
How much would you pay to buy Asset X today if the first payment occurs right away?
~~~~~~~~~~~~~~~~~~
Probably, a professional finansist can solve this problem faster than me,
but I can explain the solution better for a non-professional reader.
The question is as follows:
If you have enough amount of money Y, what is better for you:
deposit this amount Y "all in one time" today into a bank at 12% compounded quarterly
or to buy today an asset X for Y dollars, from which you will deposit
$100,000 every 3 months to a bank at 12% compounded quarterly?
First option generates the amount of A = 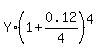 = = 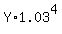 = 1.125509*Y dollars in one year.
Second option works as an Annuity Due saving plan and generates the amout
B = = 1.125509*Y dollars in one year.
Second option works as an Annuity Due saving plan and generates the amout
B = 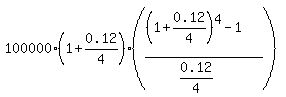 = = 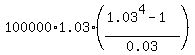 = $430913.58 (rounded) in one year.
Therefore, the reasonable value/price to buy the asset X for one year is no more than
Y = = $430913.58 (rounded) in one year.
Therefore, the reasonable value/price to buy the asset X for one year is no more than
Y = 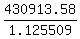 = $382861.07 dollars.
Thus, we calculated the reasonable value/price to buy the asset X for one year.
Next, let's consider more longer time intervals of n = 3, 5, 10, 20, 50 and 100 years.
We should calculate A(n) and B(n) using the formulas
A(n) = = $382861.07 dollars.
Thus, we calculated the reasonable value/price to buy the asset X for one year.
Next, let's consider more longer time intervals of n = 3, 5, 10, 20, 50 and 100 years.
We should calculate A(n) and B(n) using the formulas
A(n) = 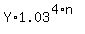 , B(n) = , B(n) =  and the ratio Y(n) =
and the ratio Y(n) = 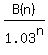 , which is the reasonable value/price to buy the asset X for n year.
The table for the values of n, B(n) and Y(n) is shown/computed below
n Y(n) B(n)
-----------------------------------------
1 430914 382861
3 1461779 1025262
5 2767649 1532380
10 7766330 2380822
20 3310039 3110679
50 1264688299 3424038
100 468384665935 3433308
From the table, it is seen that the values of B(n) raise significantly for n = 1, 3, 5, 10, 20 years,
but after that, for n = 50, 100 years tends to some limit (to stabilization).
As everybody understands, the 12% percentage account is non-realistic for such long time as 20-30-50 years
- - - therefore, I made my calculations in this lesson to present you more realistic picture. , which is the reasonable value/price to buy the asset X for n year.
The table for the values of n, B(n) and Y(n) is shown/computed below
n Y(n) B(n)
-----------------------------------------
1 430914 382861
3 1461779 1025262
5 2767649 1532380
10 7766330 2380822
20 3310039 3110679
50 1264688299 3424038
100 468384665935 3433308
From the table, it is seen that the values of B(n) raise significantly for n = 1, 3, 5, 10, 20 years,
but after that, for n = 50, 100 years tends to some limit (to stabilization).
As everybody understands, the 12% percentage account is non-realistic for such long time as 20-30-50 years
- - - therefore, I made my calculations in this lesson to present you more realistic picture.
Solved.
-----------------
On Annuity Due saving plan, see my lesson
- Annuity Due saving plans and geometric progressions
in this site www.algebra.com.
|
|
|