SOLUTION: Find the values of θ between 0° and 180° such that 2cos 3θ =3sin 3θ

Algebra ->  Finance -> SOLUTION: Find the values of θ between 0° and 180° such that 2cos 3θ =3sin 3θ      Log On


   

Question 1199171: Find the values of θ between 0° and 180° such that 2cos 3θ =3sin 3θ
Found 3 solutions by math_helper, Alan3354, ikleyn:
Answer by math_helper(2461) About Me  (Show Source):
You can put this solution on YOUR website!
  

Where the graph crosses zero, the two terms are equal. The zeros highlighted are in radians, so just multiply each x value shown by 180%2Fpi to get x ( =theta) in degrees.

Answer by Alan3354(69443) About Me  (Show Source):
You can put this solution on YOUR website!
Find the values of θ between 0° and 180° such that 2cos 3θ =3sin 3θ
-----------
y = 2cos(3x) - 3sin(3x)
2*sqrt(1-sin^2(3x)) = 32in(3x)
4*(1- sin^2(3x) = 9sin^2(3x)
9sin^2(3x) + 4sin^2(3x) - 4 = 0
--------
Solve the quadratic for sin(3x)
Solved by pluggable solver: SOLVE quadratic equation (work shown, graph etc)
Quadratic equation ax%5E2%2Bbx%2Bc=0 (in our case 9x%5E2%2B4x%2B-4+=+0) has the following solutons:

x%5B12%5D+=+%28b%2B-sqrt%28+b%5E2-4ac+%29%29%2F2%5Ca

For these solutions to exist, the discriminant b%5E2-4ac should not be a negative number.

First, we need to compute the discriminant b%5E2-4ac: b%5E2-4ac=%284%29%5E2-4%2A9%2A-4=160.

Discriminant d=160 is greater than zero. That means that there are two solutions: +x%5B12%5D+=+%28-4%2B-sqrt%28+160+%29%29%2F2%5Ca.

x%5B1%5D+=+%28-%284%29%2Bsqrt%28+160+%29%29%2F2%5C9+=+0.480506146704084
x%5B2%5D+=+%28-%284%29-sqrt%28+160+%29%29%2F2%5C9+=+-0.924950591148529

Quadratic expression 9x%5E2%2B4x%2B-4 can be factored:
9x%5E2%2B4x%2B-4+=+%28x-0.480506146704084%29%2A%28x--0.924950591148529%29
Again, the answer is: 0.480506146704084, -0.924950591148529. Here's your graph:
graph%28+500%2C+500%2C+-10%2C+10%2C+-20%2C+20%2C+9%2Ax%5E2%2B4%2Ax%2B-4+%29

sin(3x) = ~0.480506
3x = 28.718
x = ~ 9.57282, 170.4272 degs
----------
sin(3x) = ~-0.92495
3x = -22.5536 degs = 337.446 degs
=============
Can you do the rest? And convert to radians?
I have a bad cold, and this is making me dizzy.

Answer by ikleyn(52787) About Me  (Show Source):
You can put this solution on YOUR website!
.
Find the values of θ between 0° and 180° such that 2cos 3θ =3sin 3θ
~~~~~~~~~~~~~~~ 

We start from this given equation

    2*cos(3θ) = 3*sin(3θ).     (1)



Looking in it, we see that cos(3θ) =/= 0  (since 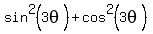sin%5E2%283theta%29+%2B+cos%5E2%283theta%29 = 1).



Therefore, we can divide both sides by cos(3θ).  Doing so, from (1) we get

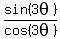    sin%283theta%29%2Fcos%283theta%29 = 2%2F3,  or  tan(3θ) = 2%2F3.    (2)


Hence,  3θ = 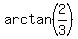arctan%282%2F3%29 = 33.69 degrees is one of several possible solutions for 3θ,
which gives  θ = 33.69/3 = 11.23 degrees.



Since the tangent function is periodical with the period of 180 degrees, 
there are other solutions to equation (2)

    3θ = 33.69+180 = 213.69 degrees and  3θ = 33.69+360 = 393.69 degrees.    (3)



From (3), it gives two other solutions for θ in the interval  [0,180] degrees.


These two additional solutions are  213.69/3 = 71.23 degrees  and  393.69/3 = 131.23 degrees.



ANSWER.  In the given interval [0,180] degrees, there are three solutions to the given equation

         θ = 11.23 degrees;  θ = 71.23 degrees  and  θ = 131.23 degrees.

Solved   (in a way as it is expected and as it should be done).