Question 1198534: Concerning negative exponents, why is the reciprocal of a fraction a positive one in the numerator? Instead of a negative one.
e.g.
6^-3 = 1 / 6^3 vs. 6^-3 = -1 / 6^3
Found 3 solutions by MathLover1, MathTherapy, math_tutor2020:
Answer by MathLover1(20849)   (Show Source): (Show Source):
Answer by MathTherapy(10552)   (Show Source): (Show Source):
You can put this solution on YOUR website!
Concerning negative exponents, why is the reciprocal of a fraction a positive one in the numerator? Instead of a negative one.
e.g.
6^-3 = 1 / 6^3 vs. 6^-3 = -1 / 6^3
6-3 =  vs. 6-3 = vs. 6-3 = 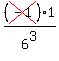 6-3 =
6-3 =  = = 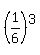 .
As seen above, the 6 in the numerator and the 1 in the denominator are BOTH positive. They can't,
all of a sudden, become negative. Then, they TRADE PLACES, but DEFINITELY remain positive.
They can't, all of a sudden, become negative.
Now, if we had: (- 6)-3, then that's the same as: .
As seen above, the 6 in the numerator and the 1 in the denominator are BOTH positive. They can't,
all of a sudden, become negative. Then, they TRADE PLACES, but DEFINITELY remain positive.
They can't, all of a sudden, become negative.
Now, if we had: (- 6)-3, then that's the same as: 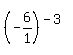 , which would then be: , which would then be: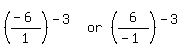 . .
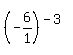 then becomes: then becomes:  , which can also be written as: , which can also be written as: 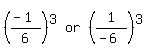 As seen above, either the numerator, 1, or the denominator, 6, can be negative, as a result of the - 6 that was given!
As seen above, either the numerator, 1, or the denominator, 6, can be negative, as a result of the - 6 that was given!
Answer by math_tutor2020(3817)   (Show Source): (Show Source):
|
|
|