If you mean negative signs by those underscores, then what you want to
simplify is this:
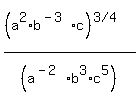
However with 6 unknowns, we cannot be sure there is any way to determine
p, q and r, so that there will be just one answer for p+2q-r.
Fraction exponents are a bummer, so let's clear the fraction exponent by
raising both sides to the 4 power:
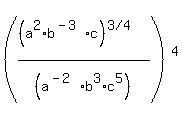
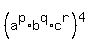
Subtract exponents of like bases to divide on the left side:
Divide both side by the left side to get 1 on the left
Subtract exponents of like bases to divide on the right side:
Maybe your teacher thought you could set all those exponents = 0,
so we would have unique solutions for p,q,r, so we could find
the value of p+2q-r to be -11/4. But that is only one solution.
For a = 1, b = 2, c = 3, p = 4, q = 5, then r≈-10.71702997,
then p+2q-r = 24.71702997 approximately.
But if a = 2, b = 3, c = 4, p = 5, q = 6, r≈-10.71702997,
then p+2q-r = -13.91541407 approximately.
There are infinitely many values possible for p+2q-r.
You should remind your teacher that we can't just assume that the
exponents of a, b, and c are equal to 0, just because the left side
is 1. a, b, and c would have to be given.
Edwin
