SOLUTION: log 2 (x-2) + log 2 (x+1) = 2

Algebra ->  Finance -> SOLUTION: log 2 (x-2) + log 2 (x+1) = 2      Log On


   

Question 1196707: log 2 (x-2) + log 2 (x+1) = 2
Found 3 solutions by josgarithmetic, MathTherapy, greenestamps:
Answer by josgarithmetic(39621) About Me  (Show Source):
Answer by MathTherapy(10555) About Me  (Show Source):
You can put this solution on YOUR website!
log 2 (x-2) + log 2 (x+1) = 2
This appears to be base 2, and it seems as though you need this solved for x. If so, you need to communicate better!

It'd then be: 

If the above is true, then x = 3  or x = - 2, but - 2 is EXTRANEOUS, so the only solution would be: x = 3.

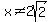If the above is true, then x+%3C%3E+2sqrt%282%29, as the other person states!

Answer by greenestamps(13203) About Me  (Show Source):
You can put this solution on YOUR website!


log%282%2C%28x-2%29%29%2Blog%282%2C%28x%2B1%29%29=2

A sum of logs is the log of the product:

log%282%2C%28x%5E2-x-2%29%29=2

x%5E2-x-2=2%5E2=4
x%5E2-x-6=0
%28x-3%29%28x%2B2%29=0
x=3 or x=-2

But x = -2 is invalid because we would have to take the logarithm of a negative number.

ANSWER: x=3

CHECK: