Question 1196259: In 2007, the population of a certain country per square mile of land area was 83. In 2000, the person per square mile population was 79.5 . Assume the relationship between years and persons per square mile is a linear relationship.
a. Write an equation, in slope-intercept form, describing the relationship between year and persons per square mile. Use ordered pairs of the form (x,y) , where x is the number of years past 2000 and y is persons per square mile.
b. Use this equation to predict the person per square mile population in 2020 .
Answer by ikleyn(52784)   (Show Source):
You can put this solution on YOUR website! .
In 2007, the population of a certain country per square mile of land area was 83.
In 2000, the person per square mile population was 79.5 .
Assume the relationship between years and persons per square mile is a linear relationship.
(a) Write an equation, in slope-intercept form, describing the relationship between year
and persons per square mile. Use ordered pairs of the form (x,y) ,
where x is the number of years past 2000 and y is persons per square mile.
(b) Use this equation to predict the person per square mile population in 2020 .
~~~~~~~~~~~~~~~~~~~
Slope-intercept form is y = mx + b. (1)
In this equation, "m" is the slope.
The ordered pairs are (0,79.5) and (7,83).
In pair (0,79.5), the zero represents the current (starting) year 2000.
In pair (7,83), the "7" represents the year 2007, 7 years after 2000.
The slope is the ratio m =  =  =  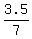= 0.5.
The slope 0.5 means that every year, the population density per square mile rises
with the rate of 0.5 of a person per square mile per year.
So, we just know that in formula (1) m = 0.5.
The value of "b" in formula (1) is the starting population of 79.5 in the starting year of 2000.
So, the formula now, in its final form is y = 0.5*x + 79.5, (2)
and it represents/expresses the population density per square mile x years after 2000.
To predict the population density in the year 2020, first calculate the number of years from the year 2000.
It is 2020 - 2000 = 20.
Now substitute x= 20 into the formula (2). You will get
y = 0.5*20 + 79.5 = 10 + 79.5 = 89.5 persons per square mile.
The problem is just fully solved.
|
|
|
