Question 1195860: If money is worth 12% per annum, compounded monthly, how long will it take the principal P to become four times the original value?
Answer by ikleyn(52781)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
If money is worth 12% per annum, compounded monthly,
how long will it take the principal P to become four times the original value?
~~~~~~~~~~~~~~~~~~
The problem's formulation is INCORRECT, since the terms are used incorrectly.
The correct formulation is as follows:
If an account  12% per annum, compounded monthly,
how long will it take the principal P to become four times the original value? 12% per annum, compounded monthly,
how long will it take the principal P to become four times the original value?
In this formulation, the solution is below.
Write equation, as you read the problem, for the account, which grows as described
4P = 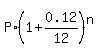 ,
where P is the principal and n is the number of months (= the number of compounding periods)
Cancel P in both sides to get
4 = ,
where P is the principal and n is the number of months (= the number of compounding periods)
Cancel P in both sides to get
4 = 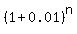 ,
or
4 = ,
or
4 = 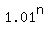 .
Take logarithm base 10 of both sides
log(4) = n*log(1.01),
n = .
Take logarithm base 10 of both sides
log(4) = n*log(1.01),
n = 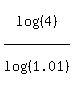 = 139.32 months.
Round the months to the closest larger integer in order for the bank
would be in position to make the last compounding.
ANSWER. 140 months, or 11 years and 8 months. = 139.32 months.
Round the months to the closest larger integer in order for the bank
would be in position to make the last compounding.
ANSWER. 140 months, or 11 years and 8 months.
Solved.
////////////////
The term " the money is worth " is used when the money is borrowed.
In this problem, the money is  , so the relevant term is " the money EARNS ". , so the relevant term is " the money EARNS ".
=================
To see many other similar (and different) solved problems, look into the lesson
- Problems on discretely compound accounts
in this site, and learn the subject from there.
After reading this lesson, you will tackle such problems on your own without asking for help from outside.
Also, you have this free of charge online textbook in ALGEBRA-I in this site
- ALGEBRA-I - YOUR ONLINE TEXTBOOK.
The referred lesson is the part of this online textbook under the topic "Logarithms".
Save the link to this online textbook together with its description
Free of charge online textbook in ALGEBRA-I
https://www.algebra.com/algebra/homework/quadratic/lessons/ALGEBRA-I-YOUR-ONLINE-TEXTBOOK.lesson
to your archive and use it when it is needed.
Happy learning (!)
|
|
|