Question 1195337: A straight line L1 is reflected in the mirror line y=2x to give the image L2 whose equation is y=1/2 x+2. Find the equation of L1. Give your answer in the form ax+by=c where a, b and c are integers
Answer by ikleyn(52781)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
A straight line L1 is reflected in the mirror line y=2x to give
the image L2 whose equation is y=1/2 x+2. Find the equation of L1.
Give your answer in the form ax+by=c where a, b and c are integers
~~~~~~~~~~~~~~~~~~
First, let's find the intersection point of the mirror line y = 2x
and line L2 whose equation is y = (1/2)x+2.
For it, we should solve the system of two equations
y = 2x,
y = 0.5x + 2.
It quickly reduces to
2x = 0.5x + 2,
which gives the solution
1.5x = 2, x = 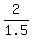 = = 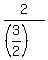 = =  .
Thus the mirror line and L2 intersect at the point with x-coordinate .
Thus the mirror line and L2 intersect at the point with x-coordinate  and y-coordinate and y-coordinate 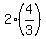 = =  .
Again, the intersection point of the mirror line and L2 is the point (x,y) = ( .
Again, the intersection point of the mirror line and L2 is the point (x,y) = ( , , ).
It means that line L1 also passes through this point (it is the reason why we found this point).
+----------------------------------------------------------------+
| At this point, half of the problem is just solved. |
| From this point, the other half of the solution starts. |
+----------------------------------------------------------------+
The mirror line y = 2x has the slope 2; it means that its angle "a" with x-axis is tan(a) = 2.
Line L2 y = (1/2)x+2 has the slope 1/2 = 0.5; it means that its angle "b" with x-axis is tan(b) = 0.5.
Let's find the angle (a-b) between these lines. We have
tan(a-b) = ).
It means that line L1 also passes through this point (it is the reason why we found this point).
+----------------------------------------------------------------+
| At this point, half of the problem is just solved. |
| From this point, the other half of the solution starts. |
+----------------------------------------------------------------+
The mirror line y = 2x has the slope 2; it means that its angle "a" with x-axis is tan(a) = 2.
Line L2 y = (1/2)x+2 has the slope 1/2 = 0.5; it means that its angle "b" with x-axis is tan(b) = 0.5.
Let's find the angle (a-b) between these lines. We have
tan(a-b) = 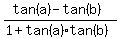 = = 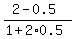 = = 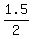 = 0.75 = = 0.75 =  .
After mirroring about y = 2x, line L2 becomes L1 with the angle with x-axis a+(a-b) = 2a-b.
I want to calculate tan(2a-b), since it gives me the slope of line L1.
I calculate tan(2a) first: it is tan(2a) = .
After mirroring about y = 2x, line L2 becomes L1 with the angle with x-axis a+(a-b) = 2a-b.
I want to calculate tan(2a-b), since it gives me the slope of line L1.
I calculate tan(2a) first: it is tan(2a) = 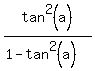 = = 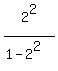 = =  .
Next, I calculate tan(2a-b). It is
tan(2a-b) = .
Next, I calculate tan(2a-b). It is
tan(2a-b) = 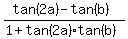 = = 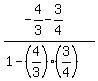 = = 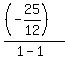 .
In the denominator, we have 1-1 = 0; it means that line L1 is vertical.
Since line L1 is vertical and passes through the point ( .
In the denominator, we have 1-1 = 0; it means that line L1 is vertical.
Since line L1 is vertical and passes through the point ( , , ), its equation is
x = ), its equation is
x =  ,
or
3x = 4.
ANSWER. An equation of line L1 in the requested form is 3x = 4, or (which is the same) 3x + 0*y = 4. ,
or
3x = 4.
ANSWER. An equation of line L1 in the requested form is 3x = 4, or (which is the same) 3x + 0*y = 4.
Solved.
-------------------
This problem is of a Math Circle level.
|
|
|