SOLUTION: Solve the equation 12^x*24^y=216

Left side is

     = .


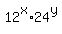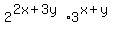Right side is

    216 =  = .


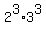So, equation is

     = .


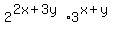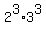Due to uniqueness of the decomposition of integer numbers into the product of primes, it implies

    2x + 3y = 3,    (1)

     x +  y = 3.    (2)


So, we have a system of two equations.
It can be easily solved by Substitution or by Elimination.


Let's do it using substitution x = 3 - y from equation (2).

Then equation (1) will give you

    2(3-y) + 3y = 3

    6 - 2y + 3y = 3

           y    = 3 - 6 = -3.


Then from (2),  x = 3 - y = 3 - (-3) = 6.


ANSWER.  x = 6,  y = -3.


You can make check on your own to convince yourself that the answer is correct.

    //  I did such check for myself.

    Alan made right notice that in the form, as the problem is worded, printed, posted and presented, 
    it has infinitely many solutions in real numbers x, y.


    But, surely, the meaning of the problem is different, and in order for the meaning was restored,
    the problem's formulation should be changed.


    The correct problem's formulation is


      +------------------------------------------------------------------------+
      | Find solution/solutions of equation  12^x*24^y=216  in integer numbers.|
      +------------------------------------------------------------------------+


    In this form, my solution above works and produces a unique answer.