Question 1194694: A light is placed on the ground 30 ft. from a building. A man 6 ft. tall walks
from the light toward the building at the rate of 5 ft.per sec. Find the rate
at which the length of his shadow on the wall is changing when he is 15
ft. from the building.
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! Here is the man, 6 ft tall, walking towards the light
on a horizontal ground surface, shown when he is at a distance x (in ft) from the light, projecting a shadow with a length s (in ft) on the wall:

If we count time from the moment  when the man starts walking fron the light, when the man starts walking fron the light,
 with with  in seconds. in seconds.
There are two similar right triangles, so
 --> --> 
and if we want  as a function of as a function of 
 --> --> 
The rate of change of a function with its variable is the derivative of the function, so we could write
 and then and then
calculate the value of 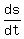 when when <--> <-->  as as
 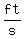
which means the shadow's length is decreasing at  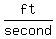 at the instant the man is at 15 ft from the light. at the instant the man is at 15 ft from the light.
Alternately, we could write  and knowing that and knowing that  as long as the man is walking between light and building as long as the man is walking between light and building
regardless of how we count the time we could calculate 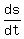 , ,
without caring how long the man has to walk to get 15 ft from the light, we calculate
 and for and for   and and  to get the same result. to get the same result.
|
|
|