SOLUTION: A light at eye level stands 20 ft. from a house and 15 ft. from the path leading from the house to the street. A man walks along the path at 6 ft.per sec. How fast does his shado

        +------------------------------------------------------+
        |        The mathematical model is the TOP VIEW        |
        |    from the bird flight height to the Earth surface. |
        +------------------------------------------------------+


So, make a sketch following my wording description.



            You are a bird now, which flights very high 
            and looks at the Earth surface from the top.



You see the Earth surface as a plane; it would be better if you imagine the Earth surface 
as a coordinate plane.

Let the coordinate axis y=0 represents the wall of the house (x-axis).

The path leading from the house to the street is y-axis x=0; or more precisely, 
the positive ray along the y-axis

The light source is located at the point L = (15,20): 15 ft from the path (from y-axis)
and 20 ft from the wall (from x-axis).


As a bird, you see the person from the top at the point P = (0,5): at the path, which is 
y-axis, and it gives you first coordinate x= 0; and 5 ft from the wall,
which gives you the second coordinate y= 5.

Connect the point L (light source) and point P (the person) by a straight line
and continue this line till its intersection with the wall (with x-axis).

This intersection represents the  SHADOW position  of the person at the wall.
In this problem, your goal is to find x, based on the rest of data.


OK.  Now you can easily see in your sketch two similar right angled triangles.

One triangle has the legs 15 ft and 15 ft; the other triangle has the legs 5 ft and 5 ft.

So, the position of the shadow x at the time moment is x= 5 ft.


        But you should consider this picture in dynamics.


In dynamics, the leg of 15 ft, perpendicular to the wall, is changed in time as 15+6t feet,
while the leg of 5 feet, perpendicular to the wall, is changed in time as 5-6t.


    Here, OBVIOUISLY, time t is counted starting from the moment 
              when the person is 5 ft from the wall.


Hence, from the triangles similarity, you can write this proportion

     = ,

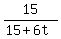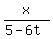where x is your sought coordinate: the shadow position.



From the proportion, you get

    x = 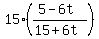      (1)

Now all you need is to find the derivative x'(t) at the time moment t= 0.


This derivative is the speed of moving the shadow along the wall.



The rest is simple arithmetic, which I leave to you to complete the solution to the end.


Again, to complete, you should calculate the derivative x'(0), i.e. find x'(t)
from equation (1) and substitute there t= 0.