Question 1191366: Suppose that $2300 is invested at 4.7% annual interest rate, compounded monthly. How much money will be in the account in (A)8 MONTHS and (B)4 years? round to the nearest cent.
Found 2 solutions by dezbee2008, ikleyn:
Answer by dezbee2008(5)   (Show Source): (Show Source):
You can put this solution on YOUR website! We will be using the formula  where: where:
A is the total accrued amount
P is the principle ($2300)
R is the rate (4.7/100 = 0.047)
N is the number of times compounded (12 months)
T is the time (in years, in this case we will use 2/3 for 8 months and 4 for 4 years)
After 8 Months
Write the formula: A=P(1+r/n)^nt
Plug in the numbers: A=$2300(1+.047/12)^(12)(2/3)
Multiply the exponents: A=$2300(1+.047/12)^8
Divide the fraction in the parenthesis: A=$2300(1+.0039)^8
Add in the parenthesis: A=$2300(1.0039)^8
Solve the exponent: A=$2300(1.0316)
Finish the problem: A=$2372.68
After 4 Years
Write the formula: A=P(1+r/n)^nt
Plug in the numbers: A=$2300(1+.047/12)^(12)(4)
Multiply the exponents: A=$2300(1+.047/12)^48
Divide the fraction in the parenthesis: A=$2300(1+.0039)^48
Add in the parenthesis: A=$2300(1.0039)^48
Solve the exponent: A=$2300(1.2054)
Finish the problem: A=$2774.70
Answer by ikleyn(52781)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Considering the answer by @dezbee2008 for 8 months, I got another number.
My number is 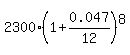 = 2373.06 dollars. = 2373.06 dollars.
The difference is not very significant, but there is an important note about it.
When you make such calculations, do not round
intermediate numbers on the way: round the answer at the END, ONLY.
Otherwise, you will make errors, even without knowing, what and where are their causes/sources.
|
|
|