SOLUTION: Reduce the equation 169(x-1)^2+144(y-3)^2=24336 into standard form then find the coordinates of the center, the foci, the endpoints of the major and minor axes as well as the endpo

Algebra ->  Finance -> SOLUTION: Reduce the equation 169(x-1)^2+144(y-3)^2=24336 into standard form then find the coordinates of the center, the foci, the endpoints of the major and minor axes as well as the endpo      Log On


   

Question 1190955: Reduce the equation 169(x-1)^2+144(y-3)^2=24336 into standard form then find the coordinates of the center, the foci, the endpoints of the major and minor axes as well as the endpoints of each latus rectum.
Answer by greenestamps(13200) About Me  (Show Source):
You can put this solution on YOUR website!


By posting this set of 10 similar problems, it is apparent that what you want us to do is complete your whole assignment for you.

That is not our purpose here. Our purpose is to help YOU learn how to work the problems.

I will give you a detailed explanation of the process for working the problems; then I will work this one example for you. Then I will answer your other questions by referring you to this response from me.

If you try the other problems on your own and are not sure of your answers, post them (each separately) showing the work you did and the answers you got, and we can help you if you need more help, or let you know if your work is good and your answers are right.

--------------------------------------------------------------------------------

There are two forms of the standard equation for an ellipse, depending on whether the major axis is horizontal or vertical:

Horizontal major axis: %28x-h%29%5E2%2Fa%5E2%2B%28y-k%29%5E2%2Fb%5E2=1
Vertical major axis: %28x-h%29%5E2%2Fb%5E2%2B%28y-k%29%5E2%2Fa%5E2=1

In those equations...
(1) (h,k) is the center of the ellipse;
(2) a is the distance from the center to each end of the major axis;
(3) b is the distance from the center to each end of the minor axis

The distance from the center to each focus is c, where c%5E2=a%5E2-b%5E2

Note this definition of c is why we need two different standard forms of the equation of an ellipse. a%5E2-b%5E2 must be positive, so a always has to be greater than b -- i.e., a is always the semi-major axis and b is always the semi-minor axis.

The distance from each focus to each end of the latus rectum is 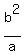b%5E2%2Fa

If the equation is given in polynomial form, you need to know how to complete the square in both variables to put the equation in one of the standard forms. Since you are working problems like this, I will assume you know how to do that.

Now we have all the information we need to work any of these problems.

--------------------------------------------------------------------------------

For this one....

169%28x-1%29%5E2%2B144%28y-3%29%5E2=24336

We need to divide both sides by 24336 to make the right side equal to 1:

%28x-1%29%5E2%2F144%2B%28y-3%29%5E2%2F169=1

%28x-1%29%5E2%2F12%5E2%2B%28y-3%29%5E2%2F13%5E2=1

This is in standard form:
the center is (h,k)=(1,3)
the semi-major axis is a=13 (in the y direction, so the major axis is vertical)
the semi-minor axis is b=12

c is sqrt%2813%5E2-12%5E2%29=sqrt%2825%29 =5
the distance from each focus to each end of each latus rectum is 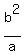b%5E2%2Fa = 144/13

ANSWERS:

center: (h,k) = (1,3)

foci: c=5 units in the positive and negative y directions from the center: (1,8) and (1,-2)

endpoints of the major axis: a=13 units in the positive and negative y directions from the center: (1,16) and (1,-10)

endpoints of the minor axis: b=12 units in the positive and negative x directions from the center: (13,3) and (-11,3)

endpoints of the latus rectum: b^2/a=144/13 units in the positive and negative x directions from each focus (note the major axis is vertical; so each latus rectum is a horizontal segment):
(1+144/13,8), (1-144/13,8), (1+144/13,-2), (1-144/13,-2)

---------------------------------------------------------------------------

Use that example to work your other problems.

And be sure to re-post if you need more help.