Question 1190897: Sam jogged to Larry's house at 8 miles per hour and borrowed Larry's scooter, riding back at 20 miles per hour. If the round trip took 7 hours, how far is it to Larry's house? Write a distance equation
Found 6 solutions by ikleyn, Theo, Alan3354, greenestamps, MathTherapy, josgarithmetic:
Answer by ikleyn(52781)   (Show Source):
Answer by Theo(13342)  (Show Source):
You can put this solution on YOUR website! rate * time = distance
for sam jogging:
rate * time = distance becomes 8 * x = distance
x = the time it took him to get to larry's home.
for sam riding back on larry's scooter:
rate * time = distance becomes 20 * y = distance.
y = the time it took him to get home.
your original two equations are:
8 * x = distance
20 * y = distance
the total time for the round trip was 7 hours.
this means that x + y = 7
solve for y to get:
y = 7 - x
the equations becomes:
for sam jogging:
8 * x = distance
for sam riding larry's scooter:
20 * (7 - x) = distance
your two equations are now:
8 * x = distance
20 * (7 - x) = distance
simplify the second equation and leave the first equation as is to get:
8 * x = distance
140 - 20 * x = distance
since distance = 8 * x in the first equation, replace distance with that in the second equation to get:
140 - 20 * x = 8 * x
add 20 * x to both sides to get:
140 = 28 * x
divide both sides by 28 to get:
5 = x
since x + y = 7, then y must be equal to 2.
your two original equations were:
8 * x = distance
20 * y = distance
replace x with 5 and y with 2 to get:
8 * 5 = 40
20 * 2 = 40
the distance is equal to 40 miles each way.
that would be a total of 80 miles round trip.
if you had added the distances together, then the round trip equation would have been:
8 * x + 20 * y = 80
with x = 5 and y = 2, the equation would have bvecome:
8 * 5 + 20 * 2 = 80
simplify to get:
40 + 40 = 80 which becomes 80 = 80, confirming the values of x and y are good.
Answer by Alan3354(69443)  (Show Source):
You can put this solution on YOUR website! Sam jogged to Larry's house at 8 miles per hour and borrowed Larry's scooter, riding back at 20 miles per hour. If the round trip took 7 hours, how far is it to Larry's house? Write a distance equation
-----------------
The average speed of a round trip is 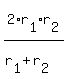 where r1 and r2 are the 2 speeds.
----------
= 2*8*20/(8+20) = 320/28 = 80/7 mi/hr
------
d = r*t = (80/7)*7 = 80 miles RT, 40 miles each way
======================
The formula is similar to parallel work, parallel resistance, etc. and is easy to remember.
Answer by greenestamps(13200)  (Show Source):
You can put this solution on YOUR website!
Ignoring the "write a distance equation" instruction in your post, here is a fast and easy way to solve this kind of problem.
The ratio of speeds for the two legs of the trip is 8:20 = 2:5.
Since the distances for the two legs are the same, that means the ratio of times spent at the two speeds is 5:2.
Since the total time was 7 hours and the ratio of times on the two legs is 5:2, he spent 5 hours jogging and 2 hours riding.
So the distance on each leg is 5*8=40 miles, or 2*20=40 miles.
Answer by MathTherapy(10552)  (Show Source):
You can put this solution on YOUR website!
Sam jogged to Larry's house at 8 miles per hour and borrowed Larry's scooter, riding back at 20 miles per hour. If the round trip took 7 hours, how far is it to Larry's house? Write a distance equation
A more appropriate equation to form in order to get straight to the answer is one of TIME.
Let distance to Larry's house be D
Then we get the following TIME equation: 
5D + 2D = 280 ------ Multiplying by LCD, 40
7D = 280
Distance to Larry's house, or 
Answer by josgarithmetic(39617)  (Show Source):
|
|
|
