Question 1190768: Randy can invest up to $40,000. As his financial advisor, you recommend that he place at least $10,000 in Account A yielding 2% and at most $20,000 in Account B yielding 5%. (i) Using x to denote the amount of money invested in Account A and y to denote the amount of money invested in Account B, write a system of linear inequalities that describes the possible amounts of each investments. Assume x and y are in thousands of dollars. [4]
(ii) Graph the system of inequalities [6]
(iii) Given that the objective function can be written as I=0.02x + 0.05y (where I represents income), determine how much money should be placed in each investment so that his income is
maximized.
Answer by Theo(13342)   (Show Source): (Show Source):
You can put this solution on YOUR website! x = 2% investment
y = 5% investment
constraints are:
x >= 10
y <= 20
x + y <= 40
x >= 0
y >= 0
objective function is:
profit = .02x + .05y
using the desmos.com calculator, you would:
graph the opposite of the inequalities.
the area of the graph that is not shaded is you region of feasibility.
the corner points of the region of feasibility are where yoour maximum solution lies.
evaluate the objective function at each of these corner point.
this is what the graph looks like:
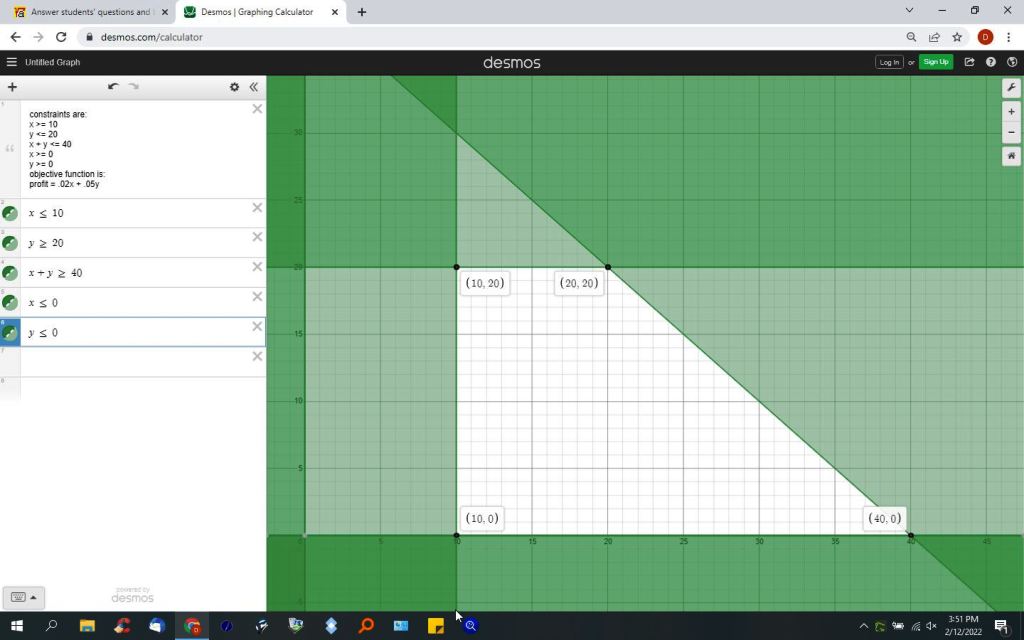
your corner points are:
(10,0)
(10,20)
(20,20)
(40,0)
at (10,0), the profit is .02 * 10 + .05 * 0 = .2 * 1000 = 200
at (10,20), the profit is .02 * 10 + .05 * 20 = 1.2 * 1000 = 1200
at (20,20), the profit is .02 * 20 + .05 * 20 = 1.4 * 1000 = 1400
at (40,0), the profit is .02 * 40 + .05 * 0 = .8 * 1000 = 800
your maximum profit is when x = 20 and y = 20.
that would be 20,000 invested in account A and 20,000 invested in account B.
.02 * 20,000 + .05 * 20,000 = 1400.
all your constraints need to be satisfied at that corner point.
at (20,20):
x >= 10 is satisfied.
y <= 20 is satisfied.
x + y <= 40 is satisfied.
x >= 0 is satisfied.
y >= 0 is satisfied.
let me know if you have any questions.
|
|
|