Question 1189224: For each of the following exercises construct 90, 95, and 99 percent confidence intervals for the
difference between population means.
1. Iannelo et al. (A-8) performed a study that examined free fatty acid concentrations in 18 lean subjects
and 11 obese subjects. The lean subjects had a mean level of 299 mEq/L with a standard error of the
mean of 30, while the obese subjects had a mean of 744 mEq/L with a standard error of the mean of 62.
Answer by math_tutor2020(3817)   (Show Source): (Show Source):
You can put this solution on YOUR website!
I'll go over how to set up the 90% confidence interval, and let you handle the other confidence intervals.
Given info:
| Lean | Obese | | Sample sizes | N1 = 18 | N2 = 11 | | Sample Means | Xbar1 = 299 | Xbar2 = 744 | | Standard Errors | SE1 = 30 | SE2 = 62 |
SE = standard error of the mean
A notation like n2 means the sample size of group 2, and does not indicate squaring. If I want to square a value, then I'd write it like n^2.
We use this formula

to determine the sample standard deviation s based on the given SE and n values.
That solves to 
So for instance, the lean group will have a sample standard deviation of roughly s1 = 127.2792 because




Also, you should find that s2 = 205.6307 approximately
Let's update the given table above
| Lean | Obese | | Sample sizes | N1 = 18 | N2 = 11 | | Sample Means | Xbar1 = 299 | Xbar2 = 744 | | Standard Errors | SE1 = 30 | SE2 = 62 | | Sample Standard Deviations | S1 = 127.2792 | S2 = 205.6307 |
Your teacher doesn't mention whether we assume the population variances are equal or not. I'll assume that we're dealing with unequal variances, which means we go for the unpooled version.
df = degrees of freedom
df = the smaller of 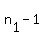 and and 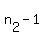 = 11-1 = 10 = 11-1 = 10
You pick the smaller sample size (in this case n2 = 11) and then subtract off 1 to get the df value.
At 90% confidence, and df = 10, the t critical value is roughly t = 1.812
I used this T table
http://www.ttable.org/
but you could use a similar table found in the back of your stats textbook.
We use a T distribution instead of a Z distribution because the sigma values aren't known.
---------------------------------------------
Let's compute the margin of error (MoE)




The margin of error is roughly 124.8046
---------------------------------------------
Next, compute the lower bound L of this confidence interval.
L = lower bound
L = (xbar1 - xbar2) - MoE
L = (299-744) - 124.804560960842
L = -569.804560960842
L = -569.80
Followed by the upper bound U
U = upper bound
U = (xbar1 - xbar2) + MoE
U = (299-744) + 124.804560960842
U = -320.195439039158
U = -320.20
---------------------------------------------
The 90% confidence interval for the difference in population means is roughly
L < mu1 - mu2 < U
-569.80 < mu1 - mu2 < -320.20
In which we can write in the format (L,U) to get (-569.80, -320.20). We are 90% confident that the value of mu1-mu2 is somewhere in that interval.
I'll let you handle the other confidence intervals (95% and 99%). The steps will nearly be the same each time; however, you'll need to update the critical t value based on the table mentioned. The other remaining values values (xbar1,xbar2,n1,n2,s1,s2) will be the same.
|
|
|