SOLUTION: Find the family of solutions of the following equation using integrating factors found by inspection. 1. 3x^2 y + (y^5 - x^3) y' = 0

The trick here is to get the left side into the expression of either the product expression of 
the differential of uv, which is:



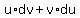or the quotient expression for the differential of 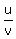, which is:



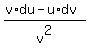We notice by inspection that the third term has x3 and the first term has 3x2dx, which is the 
differential of x3.  So we will get those two terms together and the other term
on the other side:



The product rule isn't going to work because there's a MINUS sign between the terms, not a 
PLUS sign.  So, we think of trying to make the left side into the form 

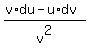, the differential form for 

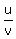The du can be the 3x2dx (with u as x3), and the v can be the y. So we'll write the y first 
in the first term:  



Now on the left we have the numerator of the differential form for .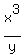

Now all we need to make the left side into the quotient differential form of 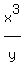 is to 
divide both sides of the equation through by y2:



So the integrating factor used here is .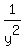



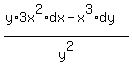
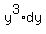Now we can integrate both sides of the equation:



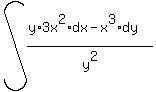
The whole left side integrates all together as the quotient 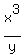, and, the right side 
integrates as 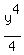 and we must add an arbitrary constant:



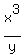
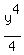
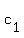Multiply through by 4y



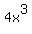
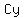[We just write C because 4 times an arbitrary constant is just another arbitrary
constant].

Edwin