Question 1187335: 5. Harris had an investment that yielded the following results over the last 4 years:
10.0%; 7.0%; 13.5%; -12.0%.
What is the arithmetic mean? The geometric mean?
Found 2 solutions by MathLover1, ikleyn:
Answer by MathLover1(20850)   (Show Source): (Show Source):
You can put this solution on YOUR website!
 %, %,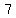 %, %,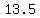 %, %,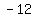 % %
to calculate arithmetic mean, write percentage as decimal, add all and divide by 
arithmetic  or or 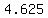 % %
geometric mean:
Geometric  , assuming , assuming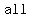 data data
values are 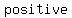
in your case , , , , ,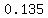 , ,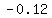 , geometric mean , geometric mean  be calculated be calculated
Geometric mean can only be calculated when all numbers have the same sign.
Geometric mean cannot be calculated for negative values.
Answer by ikleyn(52784)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Harris had an investment that yielded the following results over the last 4 years:
10.0%; 7.0%; 13.5%; -12.0%.
What is the arithmetic mean? The geometric mean?
~~~~~~~~~~~~~~~~
When the yield coefficients (the growing coefficients) of the account are given as the percentages,
from year to year, as in this given problem, which means
 = 1.10 in the 1st year; = 1.10 in the 1st year;  = 1.07 in the 2nd year; = 1.07 in the 2nd year;  = 1.135 in the 3rd year; = 1.135 in the 3rd year; 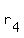 = 0.88 in the 4th year,
then the geometric mean DENOTES the geometric mean of these groving coefficients 1.1, 1.07, 1.135 and 0.88.
It MAKES SENSE, since allows to measure / (to evaluate) the average effective annual growing coefficient over the four years.
This geometric mean of the growing coefficients obeys to the usual definition
G(1.1, 1.07, 1.135, 0.88) = = 0.88 in the 4th year,
then the geometric mean DENOTES the geometric mean of these groving coefficients 1.1, 1.07, 1.135 and 0.88.
It MAKES SENSE, since allows to measure / (to evaluate) the average effective annual growing coefficient over the four years.
This geometric mean of the growing coefficients obeys to the usual definition
G(1.1, 1.07, 1.135, 0.88) =  = =  = 1.041271 = 1.04 (rounded). ANSWER
The geometric mean growing coefficient, effective over the four years, is 1.04, and the average percentage yield is about 4%. = 1.041271 = 1.04 (rounded). ANSWER
The geometric mean growing coefficient, effective over the four years, is 1.04, and the average percentage yield is about 4%.
Solved, answered and carefully/thoroughly explained.
------------------
See my lesson
- WHAT IS Geometric mean
in this site.
|
|
|