Question 1186877: Find the equation of the circle touching the lines 3x + 4y = 12, 4x +3y = 9 and having its center on the line 3x + y = 7
Found 3 solutions by Alan3354, ikleyn, Edwin McCravy:
Answer by Alan3354(69443)   (Show Source): (Show Source):
You can put this solution on YOUR website! Find the equation of the circle touching (tangent to) the lines
L1, 3x + 4y = 12,
L2, 4x +3y = 9 and having its center on the line
L3, 3x + y = 7
=========================
Find the intersection of L3 with L1 and L2. The center C is the midpoint of those 2 points.
The distance from C to L1 or L2 is the radius.
=================================
Only one circle is possible.
---
If L3 was the bisector of L1 and L2, an infinite # of circles would fit, but it is not.
If the 3 lines intersected at the same point, but L3 was not the bisector, no solution is possible.
===================
PS The problem is more interesting than a lot of the ones posted. It became clear to me after I graphed the 3 lines.
========================
Answer by ikleyn(52781)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
May be, it will sound unexpectedly to you, but there are TWO CIRCLES, satisfying the imposed conditions.
It is because the two given lines form 4 (four, FOUR) angles in the coordinate plane.
These 4 angles have two different straight lines, that are their angle bisectors - these two different
straight lines are perpendicular to each other.
The centers of the mentioned circles are intersection points of these two different lines
(angles bisectors) with the third line 3x + y = 7.
So, the problem in your post is posed/formulated INACCURATELY.
Answer by Edwin McCravy(20055)   (Show Source): (Show Source):
You can put this solution on YOUR website!
There are two solutions, as you can see below. The two black lines are
3x + 4y = 12 and 4x +3y = 9. The blue line is 3x + y = 7, and you see
that both circles have their centers on the blue line, and they touch the
two black lines. I will find the equation of the bigger circle. You
find the equation of the smaller circle. It is found the same way.
 We draw the two lines (in black) that the circles must touch (be tangent to):
We draw the two lines (in black) that the circles must touch (be tangent to):
 In order that a circle be tangent to two lines, its center must lie on one of
the bisectors of the angles between the two lines. Since the perpendicular
distance from every point on the angle bisector to both lines must be equal,
We equate their normal forms and simplify to find the equation of the two angle
bisectors
In order that a circle be tangent to two lines, its center must lie on one of
the bisectors of the angles between the two lines. Since the perpendicular
distance from every point on the angle bisector to both lines must be equal,
We equate their normal forms and simplify to find the equation of the two angle
bisectors
   Since their denominators are the same,
Since their denominators are the same,
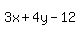  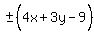 Using the +,
Using the +,
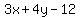  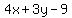
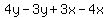  
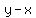   <--- one angle bisector
Using the -, <--- one angle bisector
Using the -,
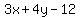  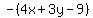
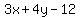  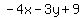
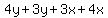  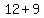
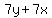  
  
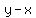   <--- the other angle bisector
Next we graph the two angle bisectors, one in green, and one in red: <--- the other angle bisector
Next we graph the two angle bisectors, one in green, and one in red:
 The centers of the circles must be on these bisectors.
We are also told that the circles must have its center on the line
3x+y=7
We draw that line (in blue):
The centers of the circles must be on these bisectors.
We are also told that the circles must have its center on the line
3x+y=7
We draw that line (in blue):
 Next we find the point where the green and blue lines intersect,
by solving this system of equations:
Next we find the point where the green and blue lines intersect,
by solving this system of equations:
 Their solution is (1,4), so that is the center of one of the circles.
Next we find the radius of the circle with that radius. We do that
by finding the perpendicular distance from the center (1,4) to either one
of the original two black lines
Their solution is (1,4), so that is the center of one of the circles.
Next we find the radius of the circle with that radius. We do that
by finding the perpendicular distance from the center (1,4) to either one
of the original two black lines
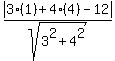 That works out to be 7/5, so the radius is 7/5 and the center is (1,4)
Therefore one answer is found by substituting in the standard form of
a circle:
That works out to be 7/5, so the radius is 7/5 and the center is (1,4)
Therefore one answer is found by substituting in the standard form of
a circle:

 <--that's one of the answers. <--that's one of the answers.
 You can find the other solution the same way by finding the center where the
blue line intersects the red line. Here is the graph of both circles
You can find the other solution the same way by finding the center where the
blue line intersects the red line. Here is the graph of both circles
 Edwin
Edwin
|
|
|