Question 1186113: Find the equation of the line parallel to 3x + 4y= 20 and at a distance 5 from this line
Found 2 solutions by Theo, robertb:
Answer by Theo(13342)   (Show Source): (Show Source):
You can put this solution on YOUR website! start with 3x + 4y = 20
subtract 3x from both sides of the equation to get:
4y = -3x + 20
divide both sides by 4 to get:
y = -3/4 * x + 5
a line perpendicular to that line will have a slope that is is the negative reciprocal of the slope of that line.
that slope will be 4/3.
if you want that perpendicular line to intersect the original line at (0,5), then the equation of that perpendicular line needs to be:
y = 4/3 * x + 5
the y-intercept of both lines is at (0,5).
this is where they will intersect.
this is what it looks like.

you now want to find another point on the perpendicular line that is 5 units from the point (0,5).
the formula for the length of a line is L = sqrt(x^2 + y^2)
when y is equal to 4/3 * x, that formula becomes L = sqrt(x^2 + (4/3 * x)^2)
when L = 5, that formula becomes 5 = sqrt(x^2 + (4/3 * x)^2)
square both sides of that equation to get 25 = x^2 + (4/3 * x)^2
simplify to get 25 = x^2 + 16/9 * x^2
multiply both sides of that equation by 9 to get 225 = 9x^2 + 16x^2
combine like terms to get 225 = 25x^2
solve for x^2 to get x^2 = 225/25 = 9
solve for x to get x = 3
when x = 3, y = 4/3 * x becomes y = 4/3 * 3 = 4.
the point on the perpendicular line that is 5 units from (0,5) will be at the point (0 + 3, 5 + 4) which is equal to (3,9).
your two points on the perpendicular line that are of interest are (0,5) and (3,9).
your line perpendicular to the perpendicular line will have a slope that is the negative reciprocal of the slope of the perpendicular line.
since the slope of the perpendicular line is 4/3, that slope will be the negative reciprocal of 4/3 = -3/4.
that is also the slope of the original line, because the perpendicular of the perpendicular is the original slope the line.
that parallel line will have a slope of -3/4 and will pass through the point (3,9).
to find the y-intercept of that line, replace x with 3 and y with 9 to get:
y = -3/4 * x + b becomes:
9 = -3/4 * 3 + b
b is the y-intercept.
this comes from the general form of the slope intercept equation of a straight line which is y = mx + b.
m is the slope
b is the y-intercept.
in the equation of 9 = -3/4 * 3 + b, solve for b to get:
b = 9 + 3/4 * 3 = 9 + 9/4 = 36/4 + 9/4 = 45/4.
the equation of the line parallel to the original line and perpendicular to the perpendicular line and passing through the point (3,9) will be:
y = -3/4 * x + 45/4.
that will look like this on the graph.
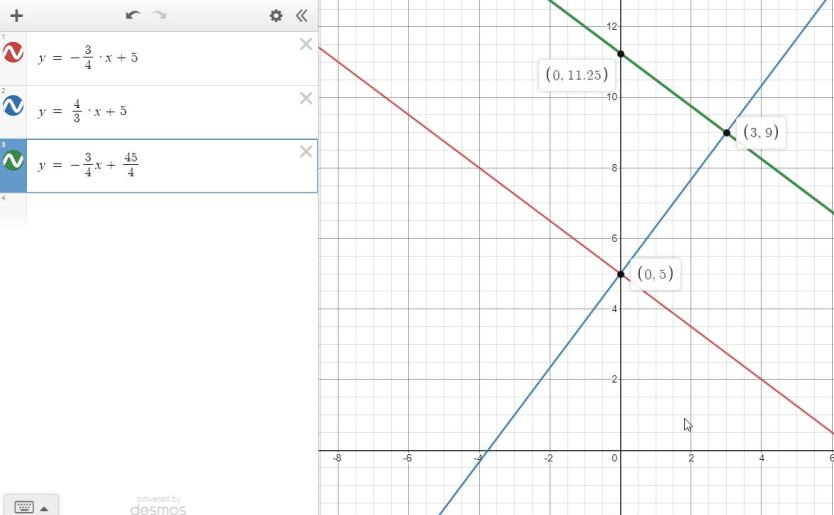
the line parallel to the original line and 5 units from the original line has the equation of y = -3/4 * x + 45/4.
45/4 is the y-intercept equal to 11.25 as shown on the graph.
the original line is red.
the line perpendicular to it is blue.
the line parallel to it is green.
your solution is that the line parallel to the original line and 5 units from it is y = -3/4 * x + 45/4.
this can also be shown as y = -3/4 * x + 11.25.
Answer by robertb(5830)   (Show Source): (Show Source):
You can put this solution on YOUR website! Let the line parallel to 3x + 4y = 20 be given by 3x + 4y = C, for some constant C.
Then the distance between the two lines is given by  , or equivalently, , or equivalently,  . .
Solving this absolute-value equation leads to C - 20 = 25 or C - 20 = -25.
===> C = 45 or C = -5.
Thus there are two lines which satisfy the given conditions, namely 3x + 4y = 45 and 3x + 4y = -5.
|
|
|