Question 1185001: A company produces a product at a cost of $6 per unit. If fixed costs are $20,000 and each unit sells at $8, at least how many units must be sold in order to earn a profit?
Found 2 solutions by ikleyn, greenestamps:
Answer by ikleyn(52832)   (Show Source):
You can put this solution on YOUR website! .
The revenue should be greater than the variable cost
8n > 20000 + 6n dollars,
where n is the number of the units produced and sold.
From the inequality,
n > 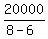 =  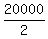= 10000.
ANSWER. At least, 10,000 units should be produced and sold.
Solved.
Answer by greenestamps(13203)  (Show Source):
You can put this solution on YOUR website!
Note the formal algebraic calculations shown by the other tutor are exactly what logic and common sense tells you.
The profit on the product is the difference between the selling price and the cost of production, which is $8-$6=$2.
To make up the fixed costs of $20,000, the number of products sold has to be greater than $20,000/$2 = 10,000.
|
|
|
